
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Затухающие электромагнитные колебания
Рассмотрим собственные колебания в контуре с сосредоточенными постоянными: емкостью 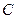 , индуктивностью
, индуктивностью  и сопротивлением
и сопротивлением 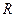
 -контур (рис. 2).Будем считать, что электрические процессы в контуре квазистационарны.
-контур (рис. 2).Будем считать, что электрические процессы в контуре квазистационарны.
 Это значит, что мгновенное значение тока
Это значит, что мгновенное значение тока 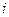 одно и то же в любом месте контура и что к мгновенным значениям электрических величин можно применять правила Кирхгофа.
одно и то же в любом месте контура и что к мгновенным значениям электрических величин можно применять правила Кирхгофа.
Согласно второму правилу Кирхгофа сумма напряжений в любом замкнутом контуре равна сумме ЭДС, встречающихся в этом контуре. В нашем случае сумме напряжения на конденсаторе  и на сопротивлении:
и на сопротивлении:  равна ЭДС самоиндукции
равна ЭДС самоиндукции  , которая возникает за счет изменения тока в катушке при перезарядке конденсатора:
, которая возникает за счет изменения тока в катушке при перезарядке конденсатора:
 (13)
(13)
Используем определение силы тока:  и закон Кирхгофа примет вид:
и закон Кирхгофа примет вид:

Разделим обе части этого уравнения на  и введем следующие обозначения:
и введем следующие обозначения:  , (
, ( - коэффициент затухания),
- коэффициент затухания),  (
( – частота собственных колебаний контура при
– частота собственных колебаний контура при  ).
).
Получим стандартный вид дифференциального уравнения затухающих колебаний, описывающего изменение со временем заряда на обкладках конденсатора в контуре 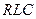 :
:
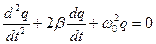 (14)
(14)
Это однородное линейное дифференциальное уравнение второго порядка с обыкновенными производными и с постоянными коэффициентами. Решение этого уравнения имеет различный вид в зависимости от соотношения между коэффициентам. Если  ,
,
то решение уравнения (14) имеет вид
 (15)
(15)
 – заряд конденсатора в начальный момент времени,
– заряд конденсатора в начальный момент времени,  – начальная фаза.
– начальная фаза.  и
и  определяются из начальных условий. Циклическая частота определяется формулой (4).
определяются из начальных условий. Циклическая частота определяется формулой (4).
Множитель перед функцией косинуса убывает со временем по экспоненциальному закону и имеет смысл амплитуды затухающих колебаний:
 (16)
(16)
Поэтому (15) есть затухающее колебание заряда на обкладках конденсатора, а (14) – соответствующее ему дифференциальное уравнение затухающих колебаний, происходящее с периодом
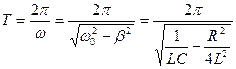 (17)
(17)
Период затухающих колебаний всегда больше периода собственных колебаний.
Разделив (15) на электроемкость 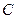 , получим напряжение на конденсаторе:
, получим напряжение на конденсаторе:
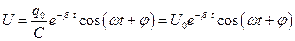 (18)
(18)
Чтобы найти величину тока, продифференцируем (15) по времени:

Умножим и разделим это выражение на 

Введем угол  , определяемый условиями:
, определяемый условиями:
 ,
,  .
.
Тогда можно записать
 (19)
(19)
Поскольку  , а
, а  ,
,  .
.
Таким образом, при наличии в контуре активного сопротивления ток опережает по фазе напряжение на конденсаторе более, чем на  и менее чем на
и менее чем на  .(при
.(при  на
на  ).
).
График функции (15) изображен на рисунке 2. Графики для напряжения и величины тока имеют аналогичный вид.
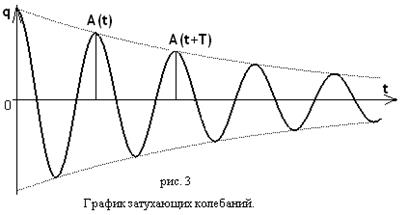
Колебательный контур часто характеризуют добротностью  , которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания
, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания
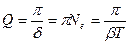 (20)
(20)
Добротность колебательной системы характеризует ее способность сохранять энергию колебаний. Она пропорциональна отношению энергии  колебаний системы в произвольный момент времени
колебаний системы в произвольный момент времени  к убыли этой энергии за период:
к убыли этой энергии за период:
 (21)
(21)
Предположим теперь, что сопротивление контура велико, так что
 .
.
В этом случае частота  , выражаемая формулой (4), будет мнимой. Это значит, электрических колебаний в контуре не будет. В этом случае решение дифференциального уравнения (14) имеет вид:
, выражаемая формулой (4), будет мнимой. Это значит, электрических колебаний в контуре не будет. В этом случае решение дифференциального уравнения (14) имеет вид:
 (22)
(22)
где  ,
,  , а
, а  и
и 
постоянные, так как  , то
, то  и
и 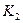 оба вещественны и положительны.
оба вещественны и положительны.
Значения постоянных определяются начальными условиями задачи:

 .
.
Это дает  ,
, 
после чего решение (22) принимает вид
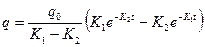 (23)
(23)

На рисунке 4 изображены графически оба слагаемых этой формулы (пунктир) и их сумма (сплошная линия). Вместо колебаний происходит апериодический разряд конденсатора. Если сопротивление контура очень велико, так что  , то
, то  и в последнем выражении можно пренебречь вторым слагаемым по сравнению с первым, а в знаменателе
и в последнем выражении можно пренебречь вторым слагаемым по сравнению с первым, а в знаменателе  по сравнению с
по сравнению с  . Тогда
. Тогда  .
.
Из сказанного видно, что для возникновения колебаний в контуре 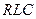 необходимо, чтобы выполнилось условие
необходимо, чтобы выполнилось условие  . Подставляем вместо
. Подставляем вместо  и
и  их значения, находим условие возникновения колебаний в виде:
их значения, находим условие возникновения колебаний в виде:  или
или  .
.
Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим
 (24)
(24)
Не нашли, что искали? Воспользуйтесь поиском: