Сложение однонаправленных гармонических колебаний

До сих пор мы изучали колебательные системы, для определения состояния которых требовалось знать закон изменения только одной величины. Для математического или физического маятников это смещение или угол отклонения . Для колебательного контура – заряд 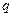и т. д. Это системы с одной степенью свободы. Каждая из этих систем характеризуется одной собственной частотой колебаний.

Числом степеней свободы называется число независимых величин, с помощью которых однозначно определяется состояние системы.

В природе существует множество колебательных систем, так или иначе связанных друг с другом. В механике, например, такую систему с двумя степенями свободы образуют два математических маятника массой и длиной , связанные невесомой пружиной с коэффициентом жесткости (рис. 10.).

В электродинамике аналогом двух связанных маятников является электрическая цепь, состоящая из двух колебательных контуров , связанных общей емкостью или связанные индуктивно (рис. 9).

Колебательные системы, между которыми имеется связь, посредствам которой они взаимодействуют друг с другом, называются связанными. Это системы с двумя степенями свободы. Для задания их состояния требуется две величины. В отличии от одиночного маятника, уединенного контура, эти системы имеют две собственные частоты.

В общем случае движение системы с двумя степенями свободы очень сложно, непохожее на простое гармоническое колебания. Однако можно показать, что при линейных уравнениях движения это сложное движение связанной системы с двумя степенями свободы может быть представлено как суперпозиция двух независимых простых гармонических колебаний, происходящих одновременно. Эти простые гармонические колебания, с помощью которых может быть представлено сложное движение связанной системы, называется нормальными или собственными колебаниями, или гармониками, или нормальными модами, или простыми модами. Частоты, соответствующие этим гармоникам или модам, называются нормальными частотами.

Задавая определенные начальные условия, можно в связанной системе возбудить колебания, соответствующие одной нормальной моде или гармонике.

Не нашли, что искали? Воспользуйтесь поиском: