Сложение взаимно-перпендикулярных колебаний

Заставим материальную точку участвовать в двух взаимно-перпендикулярных колебаниях по осям и , тогда она будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит как от соотношения частот так и от разности фаз обоих колебаний.

Пусть частоты обоих колебаний одинаковы, а уравнения их представим так:

(8)

где и – амплитуды колебаний соответственно вдоль и .

– их разность фаз .

Система представляет собой по сути дела уравнение искомой траектории в параметрической форме. Чтобы получить уравнение траектории в явном виде, исключим параметр из системы. Для этого разделим каждое уравнение системы на соответствующую ему амплитуду и получим:

Используя тригонометрическое тождество:

,

получим

.

Затем подставляя

,

получим

.

Последнее уравнение возводя в квадрат приводим к виду:

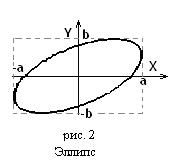
(9)

Из аналитической геометрии следует, что это уравнение эллипса с произвольно ориентированными осями, вписанного в прямоугольник со сторонами и , ограничивающего пространство, в котором совершаются колебания (рис. 2). Ориентация относительно осей зависит от разности фаз .

Рассмотрим случай , где В этом случае система уравнений (8) с помощью формулы приведения преобразуется к виду:

(10)

Поделим одно уравнение на другое и выразим :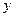

(11)

Это значит, что точка движется по прямой. При или точка совершает гармоническое колебание с частотой и

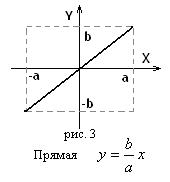
амплитудой вдоль прямой (рис. 3).

При или точка совершает колебания вдоль прямой (рис. 4.).

Если , то используя формулу приведения система уравнений приведем к виду:

(12)

Выразим уз уравнений и 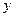, возведем каждое уравнение в квадрат и, сложив их, получим:

(13)

То есть точка движется по эллипсу (рис. 5), оси которого совпадают с осями координат, а полуоси равны и . При этом, если , то точка движется по часовой стрелке, если 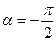, то против часовой стрелки.

Если частоты взаимно-перпендикулярных колебаний отличаются на малую величину 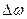, то можно считать, что они происходят с одинаковой частотой, а разность фаз медленно меняется: . В этом случае траектория будет медленно меняться, последовательно проходя все этапы, показанные на рис. 2 – 5.

Рассмотрим случай, когда частоты складываемых колебаний отличаются в два раза, например , .

Тогда система уравнений (8) примет вид:

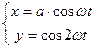
Используя формулу косинуса двойного угла, получим уравнение параболы:

(14)

Уравнение траектории – парабола (рис. 6)

В случае, когда частоты взаимно-перпендикулярных колебаний неодинаковы и кратны: , траектория результирующего движения имеют вид довольно сложных кривых, называемых фигурами Лиссажу, вписанных в прямоугольник , ограничивающий колебания по осям X и Y. При этом количество точек касания фигуры Лиссажу по горизонтали равно , а по вертикали – .

СТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ

ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА

Электронный осциллограф используют для исследования быстропеременных периодических процессов. Например, с помощью осциллографа можно измерить силу тока и напряжение, рассмотреть их изменение во времени. Можно измерять и сравнивать частоты и амплитуды различных переменных напряжений. Кроме того, осциллограф при применении соответствующих преобразователей позволяет исследовать неэлектрические процессы, например, измерять малые промежутки времени, периоды колебаний и т. д. Достоинствами электроннолучевого осциллографа является его высокая чувствительность и безынерционность действия, что позволяет исследовать процессы, длительность которых порядка 10^-6 – 10^-8 с.

Основным элементом электронного осциллографа является электроннолучевая трубка. Схематическое устройство такой трубки показано на рис. 7.

Электроннолучевая трубка состоит из подогревного катода (2) и нити накала (1). За катодом расположен управляющий электрод (3) в виде сетки или цилиндра с отверстиями. Работа его аналогична работе управляющей сетки в электронной лампе. При изменении потенциала управляющего электрода относительно катода изменяется интенсивность электронного потока, тем самым проводится изменение яркости светового пятна на экране трубки.

Первый и второй аноды (4 и 5), в виде цилиндров с диафрагмами, обеспечивают необходимую скорость движения электронов и создают электрическое поле определенной конфигурации, фокусирующее электронный поток в узкий пучок (луч).

Затем сфокусированный электронный луч проходит между двумя парами взаимно перпендикулярных отклоняющих пластин. При разных потенциалах на одной из пар отклоняющих пластин луч отклоняется в сторону пластины с большим потенциалом, причем отклонение луча пропорционально величине приложенного напряжения. Вертикальные пластины (7) обеспечивают горизонтальное перемещение электронного луча по экрану, а горизонтальные (6) дают вертикальное перемещение луча. Электроннолучевая трубка заключена в стеклянный баллон, из которого выкачан воздух до давления порядка 10^{-6 мм рт. ст., и на передней части которого нанесен тонкий слой флуоресцирующего вещества. Под воздействием электронного луча экран начинает светиться.}

Кроме генератора напряжения развертки и электроннолучевой трубки в осциллографе имеются два усилителя. Один из них, предназначенный для усиления исследуемого напряжения, обычно называют вертикальным усилителем, так как напряжение с него подается на горизонтально расположенные пластины электроннолучевой трубки, которые обеспечивали вертикальное отклонение луча по экрану. Напряжение от второго усилителя подается на вертикальные пластины, обеспечивающие горизонтальное перемещение луча. Этот усилитель называется горизонтальным. Напряжение генератора развертки подается на пластины через горизонтальный усилитель.

Для исследования характера изменения электрических сигналов во времени используют специально вмонтированное в осциллограф устройство, называемое генератором развертки. Этот генератор вырабатывает пилообразное напряжение (рис. 8), которое за время линейно нарастает от нуля до максимального значения , а затем за очень малое время падает до нуля. Частоту пилообразного напряжения можно изменять с помощью рукоятки «частота развертки». Пилообразное напряжение подается обычно на вертикальные пластины. При этом луч откланяется по горизонтали на величину пропорциональную значению пилообразного напряжения в данный момент. Так как это напряжение линейно возрастает со временем, то по горизонтали луч движется равномерно, что соответствует ходу времени, и, значит, смещение луча по горизонтали пропорционально времени. Поэтому при включенном генераторе развертки горизонталь считают осью времени. При малых частотах развертки можно увидеть поступательное равномерное движение точки по горизонтали. Если частота развертки большая, то на экране видна только горизонтальная линия. Это происходит в силу инерции зрительного восприятия и послесвечения трубки. т. е. зрительно при больших частотах мы не успеваем отметить последовательное перемещение луча по экрану слева направо при увеличении напряжения_. от нуля до максимума и почти мгновенное возвращения луча в исходное положение. На каждом следующем «зубце пилы» луч движется по одному и тому же следу слева направо по горизонтали и обратно, и повторяется это с частотой равной частоте развертки.

Чтобы увидеть, как меняется со временим исследуемое напряжение, надо одновременно подать на – вход напряжение развертки, а на – вход исследуемый сигнал . Пусть к моменту времени исследуемый сигнал достигает значения , а напряжение развертки значения 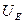. Луч, участвуя одновременно в двух взаимно перпендикулярных движениях: по горизонтали (под действием напряжения развертки) и по вертикали (под действием исследуемого напряжения ), переместится в точку 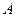(рис. 8). Если исследуемое напряжение меняется по гармоническому закону и его период совпадает с периодом развертки , то в течение времени на экране луч «выпишет» один период синусоиды. На каждом следующем зубце пилы при достижении напряжением значений и т. д. электронный луч будет попадать соответственно в те же точки и т. д. синусоиды, что и на первом зубце. Вообще, изображение на экране осциллографа будет неподвижным, если период развертки равен или в целое число раз больше периода исследуемого сигнала. При невыполнении этого условия (часто случающегося из–за нестабильности частоты генератора развертки) изображение будет «плыть» по экрану.

Для измерения периода надо на горизонтальные пластины подать исследуемое напряжение и включить генератор развертки (вход Х), подающий пилообразное напряжение на вертикальные пластины. Вращая ручку «генератор развертки», получить на экране устойчивую картину– синусоиду. Посчитать количество клеток периода синусоиды и, помножив на цену деления генератора развертки, получить период колебаний.

Не нашли, что искали? Воспользуйтесь поиском: