Броуновская коагуляция

Смолуховский [2], исходя из предположений, что:

1) частицы соударяются вследствие броуновского движения;

2) частицы слипаются при каждом столкновении;

3) частицы аэрозоля имеют сферическую форму;

4) размер всех частиц одинаков (монодисперсный аэрозоль);

5) форма и размер частиц остаются постоянными, несмотря на их коагуляцию с другими частицами, получил простое уравнение для описания процесса коагуляции:

, (9)

где dn/dt – скорость исчезновения частиц в результате коагуляции; K – константа коагуляции; n – число частиц в элементарном объеме в любой момент времени t.

Теоретически Смолуховский показал, что константа коагуляции равна:

К = 4RTC¢/ 3m_gN, (10)

где N – число Авогадро.

Для монодисперсных аэрозолей в воздухе, как показали эксперименты, константы коагуляции частиц из различного типа материала К находятся в интервале значений (0,5–2)× 10⁹ см³/с.

Уравнения (9) и (10) выполняются для частиц радиусом до 20 мкм даже при сильной турбулентности, когда e» 1000 см² /с³ (e - скорость диссипации (потери) турбулентной энергии).

Согласно Вигнеру [5] для частиц различного размера уравнение коагуляции имеет вид

, (11)

где r = (r₁+ r₂)/2; 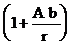– поправка, характеризующая подвижность частиц в газе (для сферических частиц в воздухе постоянная А= 0,9; b – среднее значение свободного пробега частиц); k=R/N – постоянная Больцмана.

Это уравнение показывает, что коагуляция имеет минимальное значение, когда соударяющиеся частицы имеют одинаковые размеры; частицы сильно различающиеся по размерам соединяются быстрее, чем частицы одинакового размера.

Учитывая, что константа коагуляции K=4kT/3m, уравнение скорости коагуляции для сферических частиц принимает вид

. (12)

2.2. Коагуляция частиц в ламинарном потоке [2]

В ламинарном потоке газа частицы могут сталкиваться и агломерировать вследствие различия их скоростей движения относительно друг друга. Показано, что при малом эффекте броуновской диффузии и аэродинамического взаимодействия между молекулами число частиц, контактирующих с поглощающей сферой в секунду, составляет

Ф = 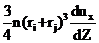, (13)

где r_i и r_j – радиусы поглощающей сферы и улавливаемой частицы соответственно; / – градиент скорости частицы в направле-нии х при ее дрейфе по направлению Z.

Градиент скорости коагуляции частиц превышает скорость броуновской диффузии при выполнении следующего условия:

, (14)

где D_p – коэффициент диффузии частицы; r_p – радиус частицы; C^' – коэффициент Каннингхема для течения со скольжением.

Видно, что даже небольшое изменение размера частицы оказывает значительное влияние на величину градиента скорости.

2.3. Коагуляция частиц в турбулентном потоке [2]

Турбулентность потока оказывает влияние на процесс коагуляции по двум механизмам. Первый из них связан с разностью скоростей флуктуаций среды в двух точках, удаленных на расстоянии (r_{o +} r_j). Этот механизм аналогичен коагуляции для случая ламинарного течения. По второму механизму коагуляция протекает вследствие разности в скоростях флуктуации частиц из-за различия в величине инерции. Поскольку инерция частицы зависит от ее размеров, первый из рассмотренных механизмов может приводить к соударениям частиц одинаковых и неодинаковых размеров; второй механизм осуществляется только при столкновении частиц разных размеров.

По первому механизму число частиц радиуса r_i, соударяющих-ся со сферой радиуса r_j за одну секунду, описывается выражением

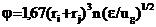, (15)

где e – скорость диссипации (потери) турбулентной энергии, см²/с³; u_g – скорость газа, см/с.

Для коагуляции по второму механизму, число столкновений для каждой частицы за 1 с равно

, (16)

где t_g и t_w – время, за которое происходит основное изменение скорости движения частицы, т. е. время релаксации частицы, и время ее блуждания (кружения) в потоке газа до момента коагуляции, соответственно.

Время релаксации определяется по формуле

t= 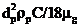, (17)

где d_р – диаметр частицы; r_р – плотность частицы; С - массовая концентрация частиц; m_g – вязкость газа.

2.4. Коагуляция аэрозолей, содержащих электрически заряженные частицы [2]

Наличие электростатических сил в условиях броуновского движения может ускорять или замедлять коагуляцию в зависимости от знака заряда частиц. Число столкновений каждой частицы за одну секунду при дополнительном действии электрических сил равно:

- для незаряженных частиц:

j=8pDrn, (18)

- для заряженного аэрозоля:

j=bj_о, (19)

где b = j/ j_о; j_о – число столкновений для каждой частицы за одну секунду в условиях броуновской коагуляции; D – характеристический размер, безразмерный; r – радиус частицы.

В случае заряженного аэрозоля индукционные силы считаются пренебрежительно малыми и для дипольного заряда при отталкивании частиц с одноименным зарядом величина b равна

b = g/ [exp(g)–1]. (20)

В случае притяжения зарядов

b = çg ç/ [1-exp(–çg ç)], (21)

где g=q_iq_j/ d_pkT; d_р – диаметр частицы; q_i , q_j – заряды частиц.

Оценки показывают, что частицы с противоположным зарядом будут коагулировать быстрее, чем нейтральные, а те, в свою очередь, быстрее, чем частицы с одноименным зарядом. В случае аэрозоля с заряженными частицами, в котором суммарный заряд равен нулю, общий эффект будет очень малым.

3. КОНДЕНСАЦИЯ И ИСПАРЕНИЕ [1, 2, 5]

Конденсация характеризует рост капель аэрозолей за счет механизма диффузии конденсирующихся паров к поверхности капли. В насыщенной или перенасыщенной паром атмосфере частицы аэрозолей выполняют роль центров конденсации. При этом размер частиц возрастает. Если степень перенасыщения паров достаточно высока (более 200 %), то пары способны конденсироваться с образованием капель и без присутствия центров конденсации.

При изучении давления насыщенных паров жидкости у ее поверхности установлено, что над выпуклой поверхностью оно больше, чем над плоской.

Математически это выражается следующей формулой [1]:

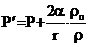, (22)

где Р¢ и Р – давление паров над выпуклой и плоской поверхностью жидкости, соответственно; a – коэффициент поверхностного натяже-ния жидкости; r – плотность жидкости; r_о – плотность паров данной жидкости; r – радиус капли.

Из этого уравнения следует, что давление насыщенных паров над сферическими каплями больше, чем над плоской поверхностью жидкости, и тем оно больше, чем меньше радиус капель. Поэтому меньшие капли будут испаряться, а на больших каплях пары будут конденсироваться, пока маленькие капли полностью не испарятся.

Предполагая, что капли жидкости находятся в стационарных условиях с парогазовой средой, Максвелл вывел уравнение для конденсации [5]

или 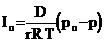, (23)

где I_o – скорость конденсации (испарения), моль/(см²∙с); D – коэффициент диффузии пара, см³/с; R - газовая постоянная, равная 0,082 л×атм/град×моль; Т – температура, К; С_о – концентрация паров у поверхности капли, моль/см³; р_о – парциальное давление паров у поверхности капли или давление пара в капле, дин/см²; С – концентрация пара на достаточно большом расстоянии от капли; р – парциальное давление пара на том же расстоянии от капли.

Фукс видоизменил это уравнение для случая, когда размер капель меньше или сравним со значением пути свободного пробега молекул в парогазовой среде. Скорость конденсации в этом случае определяется по формуле [5]

, (24)

где I – скорость конденсации или испарения, моль/см²∙с; I_o – скорость конденсации (испарения) в начальный момент времени; n=(kT/2pm)^1/2; a – коэффициент конденсации; D = b l, где l – значение пути свободного пробега в газе; b – константа, равная 1-4 (определяется экспериментально); r – радиус капли.

Коэффициент a представляет собой долю испарившихся молекул и столкнувшихся с поверхностью капли и затем адсорбированных ею, т. е. показывает, какая доля всех молекул, ударяющихся о поверхность капли, конденсируются на ней.

Для стационарной конденсации на неподвижной сферической капле в парогазовой среде изменение ее диаметра в зависимости от времени можно рассчитать по формуле [2]

, (25)

где d – текущий диаметр капли, см; d_о – начальный диаметр капли, см; D – коэффициент диффузии пара в газе, см²/с; р_о – парциальное давление пара у поверхности капли, кПа; р_u – парциальное давление пара в газовой фазе, кПа; r_a – плотность жидкости, г/см³; М – масса молекулы жидкости (М=m/N); m, N – молекулярный вес и число Авогадро.

Для конденсации капель, движущихся относительно газового потока, скорость изменения размеров капель описывается уравнением Фросслинга

, (26)

где Re_p – число Рейнольдса для частиц (Re_p=d_p(u_p–u_g) r_g/ m_g); d_р – диаметр частицы; u_p, u_g – скорость частицы и газового потока, соответственно; r_g, m_g – плотность потока и абсолютная вязкость газа, соответственно); Sc – число Шмидта (Sc=m_g/r_g×D_u, где D_u – коэффициент диффузии пара в газе).

Число Рейнольдса для частиц зависит от скорости движения частицы относительно газового потока и свойств жидкости частицы. Число Шмидта есть безразмерная величина, характеризующая отношение скорости диффузионного и конвективного переносов при постоянном числе Рейнольдса.

Для оценки скорости испарения капель, имеющих радиус 2–20 мкм, справедливо следующее соотношение [2]:

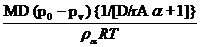= , (27)

где А=(RT/2М)^1/2; a – коэффициент конденсации или испарения, определяющий, какая доля всех молекул, ударяющихся о поверхность, конденсируется.

Для расчета скоростей испарения можно также использовать все приведенные выше уравнения, но при этом необходимо изменить знак на противоположный.

Контрольные вопросы

1. Объясните физический смысл явления седиментации аэрозольных частиц в газовой среде.

2. Сущность процесса коагуляции аэрозольных частиц в газовой среде; броуновская коагуляция.

3. Процесс коагуляции частиц в ламинарном потоке газа.

4. Объясните процесс коагуляции аэрозольных частиц в турбулентном потоке газа.

5. Объясните механизмы коагуляции электрически заряженных частиц

6. Физическая сущность процессов конденсации и испарения в газовой среде.

Не нашли, что искали? Воспользуйтесь поиском: