В ЭЛЕМЕНТАРНОМ ОБЪЕМЕ ПОТОКА ГАЗА

В ОТСУТСТВИИ ПРЕПЯТСТВИЯ [2]

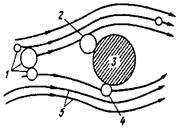
Составим материальный баланс частиц в элементарном объеме потока газа (рис. 2).

Оценим потерю частиц из потока газа в элементарном объеме за счет осаждения:

Объемная скорость потока (см³/с) Q=H_f W u_g.

Уменьшение концентрации частиц dn= n₁-n₂.

Потеря частиц из элементарного объема Qdn = –u_gH_fW dn.

Оценим количество осевших частиц:

Площадь осаждения в элементарном объеме равна

WdL= dA_d.

Объемная скорость осаждения (см³/с) u_dWdL.

Осело частиц за 1 с u_dn_d dA_d.

Таким образом, уравнение материального баланса по частицам (потеря частиц из объема равна количеству частиц осевших на площадь WdL) имеет вид:

– u_g H_f W dn = u_dn_dW dL (28)

или

– Q dn = u_d n_d d A_d. (29)

Можно наблюдать два случая:

1) отсутствие перемешивания в потоке газа:

в этом случае концентрация в объеме будет постоянной и равна входной концентрации n. Тогда уравнение баланса будет иметь следующий вид:

– dn = u_d n_d d A_d/ Q (30)

или

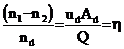, (31)

где h – эффективность удаления частиц.

2) полное перемешивание характеризуется тем, что в любой плоскости, перпендикулярной потоку газа, концентрация частиц n_d = n, и уравнение принимает вид:

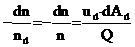, (32)

, ;

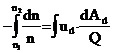n₂/n₁ = exp (–u_d A_d/ Q). (33)

Соотношение n₂/n₁ характеризует величину проскока частиц равную 1–h для любого устройства очистки. Реально скорость осажде-ния частиц в устройствах сильно зависит от размера частиц, характера потока газа, свойств газа и вида препятствия на пути их движения.

На практике процесс очистки газа от аэрозольных частиц путем осаждения их на различных препятствиях происходит за счет совокуп-ного действия эффектов инерционного осаждения, касания, гравита-ционного, диффузионного и других видов осаждения (рис. 3–5).

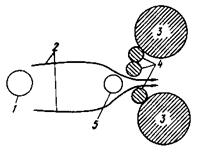
Рассмотрим отдельные механизмы улавливания частиц из потока загрязненных отходящих газов различными видами препятствий.

2. МЕХАНИЗМ ИНЕРЦИОННОГО ОСАЖДЕНИЯ ЧАСТИЦ НА ПРЕПЯТСТВИЯ [2]

В случае возникновения в газовом потоке препятствий, как, например фильтровального волокна, капель тумана и т. п., крупные частицы из-за инерции не успевают изменять направление и сталкиваются с ним, а мелкие частицы его обтекают (рис. 3). Улавливание частиц за счет инерции называется импакцией.

Эффективность инерционного улавливания h определяется как отношение числа частиц, сталкивающихся с препятствием, к числу частиц, которые столкнулись бы с препятствием, если бы линии потока газа не отклонялись им. При равномерном распределении частиц в потоке газа эффективность улавливания h равна отношению очищенной площади поверхности к площади поперечного сечения препятствия (предполагается, что все сталкивающиеся с препятствием частицы захватываются им).

Для сферического препятствия:

h_и = (у_о/r_c)². (34)

Для цилиндрического препятствия:

h_и = у_о/r_c, (35)

где у_о – расстояние от оси до граничной линии потока, для которой возможно еще соударение с препятствием; r_c – радиус препятствия.

Экспериментальные исследования показывают, что эффект инерционного осаждения частиц зависит от критериев Стокса и Рейнольдса (h = f (St, Re)). Критерий Стокса отражает относительное воздействие на частицу силы тяжести и сил вязкости газа. Критерий Стокса St = 2х/d_c, где х – путь торможения частицы; d_c – диаметр препятствия.

Число Рейнольдса для воздуха относительно препятствия определяется как

Re = u_or_gd_c/ m_g, (36)

где u_o – скорость воздуха относительно помехи, см/с; r_g – плотность газа, г/см³; d_c – диаметр препятствия, см; m_g – абсолютная вязкость газа.

Приравнивая силы инерции частицы и сопротивления воздуха движению частицы, получим уравнения ее движения:

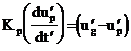; (37)

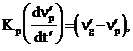(38)

где К_р (инерционный параметр) = 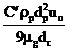; ; ; ; 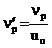; 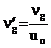t¢ = 2u_ot/ d_c; u_o – начальная скорость частицы относительно препятствия; d_c – диаметр волокна; d_c/2 – характеристи-ческий размер препятствия (для сферического препятствия равен его радиусу); u_p и n_p – составляющие скорости частицы в направлениях Х и Y соответственно; u_g и n_g – составляющие скорости газового потока относительно препятствия в направлениях Х и Y соответственно; С¢ – поправочный коэффициент Каннингхема.

Для потенциального (ламинарного) течения при значениях К_р, превышающих 0,2, экспериментально полученные величины эффективности инерционного улавливания в случае сферы приблизительно описываются соотношением [2]

h_и = [K_p/(K_p +0,7)]². (39)

В большинстве случаев теоретические решения уравнений (31) и (32) позволяют определить критическое значение К_р, ниже которого не происходит инерционного улавливания. Для цилиндра К_крит =0,125, а для сферы К_крит =0,083. Во многих работах показано, что данные значения являются теоретически предельными. В действительности же в случае турбулентного потока происходит улавливание частиц на обратной стороне препятствия и эффективность улавливания для К_р £ К_крит не равна нулю.

Как и в случае сферы, инерционное улавливание цилиндром представляет функцию параметра соударения, а режим потока определяется числом Рейнольдса для коллектора Re_c. Если Re_c <1, то поле потока вокруг цилиндра рассматривается как вязкое, а если Re_c >100, то поток вокруг цилиндра можно приближенно считать потенциальным.

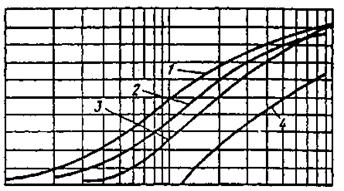
Опытная зависимость эффективности очистки газа за счет инерционного эффекта h_и от числа Стокса и Рейнольдса показана на рис. 6 и 7. Числа Рейнольдса в диапазоне 0,2<Re<150 охватывают переходную область от ламинарного к турбулентному течению газа.

Инерционный эффект осаждения частиц практически отсутствует при движении частиц размером менее 1 мкм со скоростью менее 1 м/с.

3. УЛАВЛИВАНИЕ ЧАСТИЦ ЗА СЧЕТ МЕХАНИЗМА КАСАНИЯ [2]

Эффект улавливания частиц за счет касания с препятствием (рис. 3) наблюдается при условии, что траектория частиц проходит от поверхности препятствия на расстоянии, равном или менее радиуса частицы. Эффективность очистки касанием h_к определяется соотно-шением размеров пор фильтрующего материала d_п и частиц d_р. При d_р > d_п наблюдается удаление частиц входной поверхностью фильтра (ситовый эффект) с образованием слоя осадка (см. рис. 5).

Эффективность улавливания за счет механизма касания для частицы движущейся по линии тока в ламинарном течении можно рассчитать по формуле [2]

h_к= (1+К_к)² – [ 1/(1+ K_к)], (40)

где К_к – параметр перекрывания, который определяется соотношением К_к= d_p/d_c, здесь d_p – диаметр частицы, d_c – диаметр нити.

Для турбулентного течения газа

h_к= 1+К_к – [1/(1+ K_к)]. (41)

Не нашли, что искали? Воспользуйтесь поиском: