Закон преломления света (2.1) можно записать в виде

Н.Витюк

ГЕОМЕТРИЧЕСКАЯ ОПТИКА.

ОПТИЧЕСКИЕ ПРИБОРЫ

Учебное пособие

Одесса - 2015

Методическое пособие составлено кандидатом физико–математических наук, Витюком Николаем Васильевичем - доцентом кафедры "Физика" Одесского национального морского университета.

Рецензент доктор технических наук, академик Академии наук высшей школы Украины, профессор Цымарный Валентин Александрович - заведующий кафедрой "Физика и химия" Одесского национального морского университета.

Методическое пособие одобрено кафедрой "Физика" ОНМУ.

1. Основные определения геометрической (лучевой) оптики.

Оптика изучает излучение, распространение и взаимодействие с веществом большого диапазона электромагнитных волн – от миллиметровых радиоволн до жесткого γ-излучения. К понятию об электромагнитной природе света люди подошли только в XIX в. Первоначально в оптике изучался видимый свет, испускаемый источниками света – химическими, биологическими, физическими. К физическим источникам относятся раскаленные тела и люминесцентные источники холодного света. Другие тела отражают свет и потому видимы.

Для многих практических целей можно считать, что свет действительно распространяется прямолинейно. То же самое относится и к звуковым волнам, и к радиосигналам, и к волнам на поверхности воды, и к любым другим видам волновых движений, если только длина волны λ мала по сравнению с любыми ограничениями поперечных размеров пучка а (λ << а). В таких условиях приближенно можно считать, что волны распространяются вдоль траектории, перпендикулярной к волновому фронту.

Поведение света во многих задачах удается достаточно просто и наглядно описать, используя понятия световой пучок и световой луч. Пучком называют область пространства, в пределах которой распространяется свет (или другой волной процесс). Лучом называется линия, характеризующая направление распространения света, направление распространения энергии излучения. И пучок и луч вводятся как геометрические характеристики распространения света, но уж так повелось, что пучки и лучи наделяют свойствами, им не присущими. Говорят, например, о распространении пучка или луча, о падении, преломлении, отражении пучков и лучей, об окраске световых пучков или лучей, их интенсивности и т.п. Мы не будем нарушать эту традицию, так как иначе изложение стало бы очень громоздким. Хотя луч представляет собой математическую линию, всем нам доводилось видеть световые пучки, которые дают приближенное представление о лучах. Например, пучок света от проекционного фонаря, пробивающийся сквозь запыленный воздух аудитории, очерчен лучами. Иногда мы видим солнечные «лучи», выходящие из просвета в облаках или из узкой щели в неплотно закрытой двери.

Оптические приборы, используемые в повседневной жизни и в научных исследованиях, представляют собой комбинации из линз и зеркал. Объяснение большинства оптических явлений опирается на простые законы, описывающие отражение и преломление лучей. Вместо того чтобы иметь дело с отражением, преломлением или дифракцией волновых фронтов, часто бывает легче вводить в рассмотрение лучи, перпендикулярные к волновым фронтам. Такое приближение называется геометрической (лучевой) оптикой в противоположность полному волновому рассмотрению, называемому физической оптикой. Лучевая оптика представляет собой просто удобное приближение для волновой оптики. Сами лучи лучше всего представлять себе как нормали к волновым фронтам (т.е. линии, перпендикулярные к фронтам). Если волновые фронты плоские, то лучи перпендикулярны к этим плоскостям, параллельны друг другу и проходят на равных расстояниях друг от друга. Если волновые фронты круговые (в случае двух измерений) или сферические (в случае трех измерений), то световые лучи расходятся вдоль радиусов (радиальные).

Рис.1. Лучи распространения плоских (сферических) волн.

Выходящие из источника лучи распространяются прямолинейно (рис.1) до тех пор, пока свойства среды на их пути остаются неизменными. Эти лучи непрерывны, если среда не поглощает энергии волнового движения. Интенсивность волны можно выразить качественно через число лучей, проходящих через единичную площадку. Мы пользуемся такой количественной моделью при описании электрических и магнитных полей. Однако в случае лучей света отметим, что если световые лучи расходятся, интенсивность света должна уменьшаться, если же они сходятся, интенсивность возрастает. Если волны расширяются от точечного источника в двух измерениях лучи направлены по радиусам и равномерно распределены по окружности. Поскольку длина окружности пропорциональна радиусу, а полное число лучей при увеличении радиуса остается постоянным, число лучей на единицу длины окружности должно быть обратно пропорционально радиусу. И в самом деле, интенсивность волны, расширяющейся равномерно от точечного источника в двух направлениях, обратно пропорциональна расстоянию от источника. Подобным же образом интенсивность, создаваемая точечным источником, равномерно излучающим в трех измерениях, обратно пропорциональна квадрату расстояния от источника. И на этот раз число лучей, выходящих из источника, не зависит от расстояния, но площадь поверхности сферы растет как 4π². Поэтому число лучей на единицу площади пропорционально 1/ r ².

Устройство, с помощью которого преобразуются лучи, представляет собой оптическую систему. Источник лучей (собственных или отраженных) – предмет. Лучи, идущие от предмета к системе,– входящие. После преобразования в системе получаются лучи выходящие.

Оптическая система называется идеальной, если каждому входящему в нее лучу соответствует один выходящий. При этом все входящие лучи, идущие от одной точки, пересекаются (или расходятся так, что пересекаются их продолжения), выходя из системы, в одной точке. Эта точка пересечения – изображение данной точки. Для построения изображения точки в идеальной системе достаточно построить любые два луча, идущие от этой точки. Точка пересечения выходящих лучей, соответствующих этим двум падающим, будет искомым изображением данной точки.

Лучи, выходящие из оптической системы, могут быть сходящимися или расходящимися. В первом случае они пересекутся в точке действительного изображения. Во втором – точка пересечения продолжений выходящих лучей будет мнимым изображением. Изображение предмета в идеальной системе представляет собой совокупность изображений его точек. Это точечное изображение.

2. Основные законы геометрической оптики.

Еще до установления природы света были известны следующие основные законы оптики: прямолинейного распространения света в оптически однородной среде; независимости световых пучков и их обратимости; законы отражения и преломления света.

В 1660 г. П. Ферма сформулировал общий закон распространения света – принцип Ферма, или принцип кратчайшего оптического пути (или минимального времени распространения): действительный путь распространения светового луча есть путь, для прохождения которого свету требуется минимальное время по сравнению с любым другим возможным путем между теми же точками. Для однородной среды этот принцип приводит к закону прямолинейного распространения света, так как прямая есть кратчайшее расстояние между двумя точками. Из принципа Ферма вытекают законы отражения и преломления света.

Понятием световых лучей пользуется геометрическая оптика, решающая очень важные практические задачи более простым путем, чем волновая. Но при пользовании законами геометрической оптики следует помнить, что они приближенны.

Закон прямолинейного распространения света: свет в оптически однородной среде распространяется прямолинейно.

Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их источниками малых размеров. Тщательные эксперименты показали, однако, что этот закон нарушается, если свет проходит через очень малые отверстия, причем отклонение от прямолинейности распространения тем больше, чем меньше отверстия.

Закон независимости световых пучков: эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Разбивая световой поток на отдельные световые пучки (например, с помощью диафрагм), можно показать, что действие выделенных световых пучков независимо.

Если свет падает на границу раздела двух прозрачных сред, то падающий луч I (рис. 2) разделяется на два – отраженный II и преломленный III, направления которых задаются законами отражения и преломления.

Рис.2. Падение светового луча на границу раздела двух сред.

Условились углы падения i, отражения i ₁ и преломления r отсчитывать от перпендикуляра к точке падения луча. Иногда рассматривают угол скольжения β падающего луча, дополняющий угол падения i до 90^о.

Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол i ₁ отражения равен углу падения i: (i ₁= i).

Различают отражения зеркальное и диффузное. Зеркальным называется отражение, при котором падающий на поверхность параллельный пучок лучей света остается параллельным (Рис.3,1.). Диффузным называется отражение, при котором падающий параллельный пучок рассеивается (рис.3.2).

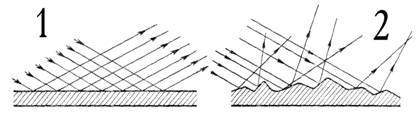
Рис.3. Виды отражения.

Соответственно различают зеркальные (достаточно гладкие) и матовые (рассеивающие) поверхности. Это относительные понятия. Одна поверхность может быть зеркальной и матовой для излучений различной длины волны (для зеркального отражения необходимо, чтобы длина световой волны была значительно меньше оптических неоднородностей среды). Даже для одного излучения матовая поверхность может стать зеркальной, если увеличить угол падения.

Закон преломления: луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:

, (2.1)

где n ₂₁ – относительный показатель преломления второй среды относительно первой. Индексы указывают, в какой среде (первой или второй) идет луч, а n ₁ и n ₂ - относительные показатели преломления этих сред относительно вакуума. Абсолютный показатель преломления показывает, во сколько раз скорость света в данной среде v меньше скорости света в вакууме c: n = c / v. Среда с большим абсолютным показателем преломления называется оптически более плотной. Скорость света в среде v, а, следовательно, и её показатель преломления n зависят от частоты. Это свойство называется дисперсией.

Закон преломления света (2.1) можно записать в виде

n ₁ sin i = n ₂ sin r. (2.2)

Из симметрии выражения (2.2) вытекает обратимость световых лучей. Если обратить луч III (рис.2), заставив его падать на границу раздела под углом r, то п реломленный луч в первой среде будет распространяться под углом i, т.е. пойдет в обратном направлении вдоль луча I. Если свет распространяется из оптически более плотной среды в менее плотную, т.е из среды с большим показателем преломления n ₁ в среду с меньшим показателем преломления n ₂ (n ₂< n ₁), например из стекла в воду, то, согласно (2.2)

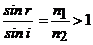
и преломленный луч удаляется от нормали, при этом угол преломления r больше, чем угол падения i, (рис.4,а). С увеличением угла падения увеличивается угол преломления (рис.4,б,в), до тех пор пока при некотором угле падения (i = i _пр) угол преломления не окажется равным π/2. Угол i _пр называется предельным углом. При углах падения i *> i _пр весь падающий полностью отражается (рис.4,г) при этом угол падения равен углу отражения.

По мере приближения угла падения к предельному интенсивность преломленного луча уменьшается, а отраженного – растет. Если i = i _пр, то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего. Таким образом, при углах падения в пределах от i _пр до π/2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

Рис. 4. Явление полного отражения

По мере приближения угла падения к предельному интенсивность преломленного луча уменьшается, а отраженного – растет. Если i = i _пр, то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего. Таким образом, при углах падения в пределах от i _пр до π/2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

Предельный угол i _пр определим из формулы (2.2) при подстановке в нее r = 90^o. Тогда

sin i _пр= n ₂ / n ₁. (2.3)

Уравнение (2.3) удовлетворяет значениям угла i _пр при n ₂< n ₁. Следовательно, явление полного отражения имеет место только при падении света из среды оптически более плотной в среду оптически менее плотную.

Явление полного отражения используется в призмах полного отражения. Показатель преломления стекла равен n ≈ 1,5 поэтому предельный угол для грани стекло – воздух i _пр= arcsin (1/1,5) ≈ 42^o. Поэтому при падении света на границу стекло – воздух при i >42^о всегда будет иметь место полное отражение. Благодаря полному отражению кажутся блестящими пузырьки газа в жидкости. Наблюдать полное отражение можно на поверхности спокойной воды, если на нее смотреть снизу. Когда ныряльщик смотрит на поверхность из-под воды под малым углом, он видит предметы, находящиеся над водой; смотря под большим углом, он увидит предметы, расположенные на дне.

Рис.5. Призмы полного отражения

Явление полного отражения используется в призмах полного отражения. На рис.5 показаны призмы, позволяющие: а) повернуть луч на 90^о, б) повернуть изображение, в) обернуть лучи. Такие призмы применяются в оптических приборах (например, в биноклях, перископах), а также в рефракгометрах, позволяющих определять показатели преломления тел (по закону преломления, измеряя i _пр, определяем относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления второй среды известен).

Явление полного отражения используется также в световодах, представляющих собой тонкие произвольным образом изогнутые нити (волокна) из оптически прозрачного материала. В волоконных деталях применяют стеклянное волокно, световедущая жила которого окружается стеклом – оболочкой из другого стекла с меньшим показателем преломления. Свет, падающий на торец световода под углами, большими предельного, претерпевает на поверхности раздела сердцевины и оболочки полное отражение и распространяется только по световедущей жиле. Такие волокна обладают большой гибкостью, их можно связывать между собой в пучки для передачи света по искривленным проходам, либо для передачи изображений из скрытых или удаленных мест. Диаметр световедущих жил лежит в пределах от нескольких микрометров до нескольких миллиметров. Для передачи изображений, как правило, применяются многожильные световоды. Световоды используются для кодирования и передачи информации, в медицине (например, диагностика желудка), для целей интегральной оптики и т.д.

3.Построение изображения в плоском зеркале.

Для построения изображения в плоском зеркале необходимо задать положение зеркала ML, глаза А и светящегося точечного источника света S (рис.6.А).

Рис. 6. Построение изображения точки (А) и предмета (В) в плоском зеркале.

Из точки S опустим перпендикуляр SL на зеркало ML и, продлив его «в глубь» зеркала (SL = S ` L), получим мнимое изображение светящейся точки S `(рис. 1.А). В этом направлении из глаза А проведем луч АS `. Соединим точку О падения луча на зеркало со светящимся источником S. Докажем, что угол падения луча на зеркало равен углу отражения (i = i <sub>1</sub>). Из равенства треугольников OLS и OLS` следует равенство углов LOS и LOS`, но Ð LOS` = Ð АОМ = Ð LOS. Из равенства Ð АОМ = Ð LOS следует равенство углов, дополняющих их до 90^о, т.е угол падения i равен углу отражения i ₁

Таким образом, глядя на зеркало вдоль луча АО, мы видим изображение точки S, полученное продолжениями лучей SL и АО, т.е. мнимое изображение S`. В геометрической оптике условились продолжения лучей (и соответственно мнимые изображения полученные пересечением продолжений лучей) изображать пунктирными линиями. Из построения следует, что длина AOS равна AOS`, следовательно, изображение любого объекта находится на таком же расстоянии за зеркалом, на каком находится предмет перед зеркалом, т.е. изображение предмета в плоском зеркале имеет натуральную величину.

Построим аналогично изображение предмета (треугольника АВС, рис.6,В) в плоском зеркале. Лучи теперь можно не строить, мы знаем, что изображением каждой точки в зеркале будет зеркально симметричная точка. Изображени е АВС мнимое (пересекаются продолжения лучей), прямое, равное, но зеркально симметричное (т.е. отражение левой стороны предмета является правой стороной изображения и т.п.). Отпечаток текста на промокательной бумаге читается с трудом – там буквы «наоборот». В зеркале изображение еще раз переворачивается и читается легко.

Однако нет правил без исключений. Если на плоское зеркало падает пучок сходящихся лучей, то после отражения они пересекутся, и точка их пересечения будет действительным изображением S источника S ₁ (рис.7), так как оно образовано действительными лучами, пересекшимися в точке S ₁ после отражения от зеркала.

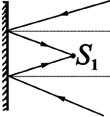
Рис.7. Получение действительного изображения в плоском зеркале.

При построении изображения в плоском зеркале следует за зеркалом построить мнимые продолжения падающего и отраженного лучей. При этом действительные лучи изображают прямой линией со стрелкой, указывающей направление хода лучей, а мнимые лучи и изображения предметов принято изображать штриховой линией. Мнимое изображение предмета всегда получается за зеркалом, а действительное – перед ним. Чтобы глаз человека увидел изображение источника света или предмета в зеркале, нужно, чтобы за зеркалом пересеклись мнимые продолжения двух различных лучей, испущенных данным источником или каждой точкой светящегося предмета от его начала до конца.

При построении изображения прямого предмета (стрелки) достаточно построить изображения его крайних точек. При построении изображений, даваемых системой зеркал, изображение, даваемое одним зеркалом, можно считать предметом или источником по отношению ко второму зеркалу, изображение, даваемое вторым, – предметом по отношению к третьему и т.д.

Если два плоских зеркала расположены под углом φ друг к другу, то количество изображений N источника света, расположенного между зеркалами, зависит от угла между ними и может быть определено по формуле:

.

Из этой формулы следует, что если угол φ =0^о, то изображений источника будет бесконечно много, а если угол φ=180^о, то изображение будет одно. Соответственно, если φ=90^о, то изображений будет три и т.д.

Плоские зеркала находят широкое применение в оптических приборах для поворота луча света, для деления его на части, для переворачивания изображения и т.д. Плоские зеркала используются в точнейших измерительных приборах – интерферометрах.

Не нашли, что искали? Воспользуйтесь поиском: