Сферические зеркала.

Поверхность тела, имеющая форму сферического сегмента, способная зеркально отражать падающий на нее свет, называется сферическим зеркалом. Если отражающая поверхность является внутренней стороной зеркала, то оно называется вогнутым, если наружной стороной, то зеркало называется выпуклым. Оптическим центром О зеркала называется центр сферы, из которой вырезан сегмент. Полюсом зеркала Р называется вершина сферического сегмента. Прямая ОР, проходящая через оптический центр и полюс зеркала, называется главной оптической осью. Любая прямая, проходящая через оптический центр О (например, АА '), называется оптической осью зеркала.

Рис.10.Отражение лучей от вогнутого зеркала.

Рассмотрим отражение света от вогнутого зеркала. Вогнутые зеркала обладают замечательным свойством собирать (фокусировать) пучок света, падающий на него параллельно оптической оси. Рассмотрим только параксиальные лучи - такие, что расстояние между ними и главной оптической осью (h) мало по сравнению с радиусом сферической поверхности R.

Если на зеркало падают лучи, параллельные главной оптической оси (рис.10), то после отражения от него все лучи сходятся в одну точку F, которая называется главным фокусом зеркала. Каждый из проведенных лучей подчиняется законам отражения света. Расстояние FР от главного фокуса до полюса зеркала принято называть фокусным расстоянием. Из построения следует, что

. (6.1)

Итак, все лучи, падающие параллельно главной оптической оси зеркала, отражаясь, проходят через главный фокус. Поскольку при явлении отражения света соблюдается закон взаимности, или обратимости, световых лучей, то можно поменять местами падающие и отраженные лучи, поместив в главном фокусе зеркала сильный источник света очень малых размеров (точечный). При этом свет, излучаемый из главного фокуса, после отражения от зеркала всегда распространяется параллельно его главной оптической оси, образуя узкий пучок. На основе этого принципа действуют многие прожекторы.

Если на зеркало падают лучи параллельно какой-либо побочной оси, то после отражения они собираются в точке А (рис.11) лежащей в фокальной плоскости, которая проходит через главный фокус зеркала и перпендикулярна к главной оптической оси.

Положение светового пятна в точке А можно приближенно определить, проведя лишь два луча. Луч, прошедший через главный фокус, должен отразиться параллельно главной оптической оси (луч, параллельный главной оптической оси, отражается через главный фокус). Кроме того, луч, падающий на полюс зеркала, должен отражаться в виде луча, симметрично расположенного по другую сторону оси. Пересечение этих двух лучей и дает возможность найти положение светового пятна А – изображения источника света. Иногда удобно пользоваться лучом, идущим через оптический центр зеркала (луч ОFP - угол его падения на зеркало равен 90^о), – он, отразившись, пойдет по той же прямой

Рис.11. Нахождение фокальной плоскости

Зная поведение лучей, отраженных от вогнутого зеркала, можно получить соотношения между расстояниями предмета (предметом будем называть источник света) и его изображения от зеркала, между величиной предмета и изображения. Для построения изображения каждой точки предмета достаточно взять любые два луча, поведение которых после отражения известно.

Пусть предмет расположен перед вогнутым зеркалом за главным фокусом на расстоянии d от полюса зеркала (рис.12). Обозначим высоту предмета, считая от оси, через Н _o.

Рис.12.Построение изображения в сферическом зеркале

Рассмотрим свет, исходящий от вершины предмета и падающий на зеркало. Проследим за ходом двух лучей: один луч падает на зеркало параллельно главной оптической оси и отражается через главный фокус, другой луч падает на зеркало через главный фокус и отражается параллельно главной оптической оси. Точка, в которой они пересекаются после отражения, будет тем местом, где получится изображение вершины предмета. Пользуясь такими чертежами, можно предсказать размеры (Н) и положение (расстояние f от изображения до полюса зеркала Р) изображения.

Однако не обязательно всякий раз для этого строить ход лучей. Из геометрических построений (рис.12) можно легко найти связь между размером H _o предмета AB и размером Н изображения B ´ A ´, а также расстояниями от предмета и изображения до зеркала.

Отношение Н к Н _о, можно получить из подобия треугольников СFР и АВF:

, (6.2)

где F – фокусное расстояние. Строго говоря, катет FР треугольника СFР несколько меньше фокусного расстояния из-за кривизны зеркала, но если предмет невелик и падающий луч (параксиальный луч!) образует с осью малый угол, то можно считать основание этого треугольника равным фокусному расстоянию F.

Из подобия треугольников А ' В ' F и DРF получаем:

. (6.3)

Это соотношение тоже является приближенным, так как катет FР треугольника DFР немного меньше фокусного расстояния. Объединяя пропорции (6.2) и (6.3), получим

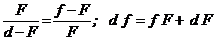
Разделим почленно на d f F. Получим для вогнутого зеркала:

. (6,4)

Из этого соотношения можно сделать заключение, что при приближении предмета к главному фокусу изображение удаляется от зеркала. Когда предмет проходит через главный фокус, действительное изображение его будет на бесконечно большом расстоянии от зеркала. Если продолжать приближение предмета к зеркалу, то появляется мнимое изображение (уже за зеркалом). Из построения (рис.13) нетрудно убедиться, что всякий раз, когда предмет находится между главным фокусом и зеркалом, должно получаться мнимое изображение.

Рис.13. Построение мнимого изображения

Как видно из рис.13, после отражения от зеркала лучи кажутся выходящими из точки их пересечения А ', расположенной за зеркалом, а изображение всегда увеличено по сравнению с предметом (если d < F). Зеркало создает лишь впечатление, что лучи исходят от мнимых точек изображения, находящегося за зеркалом.

Рис.14.Построение изображения в выпуклом зеркале.

Как видно из рис.14, лучи, падающие от предмета А на выпуклое зеркало, отражаясь, рассеивается, подчиняясь закону отражения, а их мнимые продолжения пересекаются в точке А ', которая лежит за зеркалом («внутри» его), образуя мнимое изображение. Напоминаем, что мнимые продолжения лучей и образованные их пересечением мнимые изображения обозначают пунктирными линиями.

Общие алгоритмы построения изображений в сферических зеркалах мы рассмотрим ниже.

Формулу (14.3) для выпуклого зеркала записывают в виде

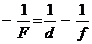. (6.4)

Объединяя формулы (6.3) и (6.4) получаем общую формулу сферического зеркала:

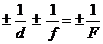. (6.5)

Здесь d – расстояние от источника света до зеркала, f – расстояние от -зеркала до изображения, F – фокусное расстояние зеркала (F = R /2, R – радиус сферы, из которой вырезано зеркало).

Правило знаков: Знак "+" ставится перед d, когда предмет действительный, перед f, когда изображение действительное, перед F, когда фокус действительный (у вогнутого, т.е. собирающего зеркала). Знак "–" ставится перед d, когда предмет мнимый, т.е. когда на зеркало падает пучок сходящихся лучей, перед f, когда изображение мнимое, перед F, когда фокус мнимый (у выпуклого зеркала).

Если d = ∞, то f = F, т.е. параллельные лучи из бесконечности, сходятся в точке фокуса на расстоянии F от зеркала. Если же источник поместить в фокусе d = F, то f = ∞, т.е. после отражения от сферического зеркала расходящийся пучок становится параллельным. Если R = ∞ (плоское зеркало), то f = – d, т.е. изображение будет мнимым, «располагаясь» симметрично за зеркалом.

Не нашли, что искали? Воспользуйтесь поиском: