Тонкие линзы. Изображение предметов с помощью линз

Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями, обычно сферическими, радиусами R ₁ и R ₂. По внешней форме линзы делятся на: 1) двояковыпуклые; 2) плосковыпуклые; 3) двояко вогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые, а по оптическим свойствам – на собирающие и рассеивающие (рис.15).

Рис.15. Виды линз (1-6).

Условные обозначения собирающей (7) и рассеивающей (8) линз.

Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами образующих поверхностей R ₁ и R _2..

Прямая, проходящая через центры кривизны A и B поверхностей линзы, называется главной оптической осью (рис.16). Для всякой линзы существует точка, называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Для простоты оптический центр O линзы будем считать совпадающим с геометрическим центром средней части линзы (это справедливо только для двояковыпуклой и двояковогнутой линз с одинаковыми радиусами кривизны обеих поверхностей; для плосковыпуклых и плосковогнутых линз оптический центр O лежит на пересечении главной оптической оси со сферической поверхностью).

Для вывода формулы тонкой линзы – соотношения, связывающего радиусы кривизны R ₁ и R ₂, поверхностей линзы с расстояниями d и f от линзы до предмета и его изображения, можно последовательно применять выражения (6.2) - (6.3) к обеим преломляющим поверхностям линзы (это предоставим сделать читателю).

Мы же для вывода формулы тонкой линзы воспользуемся принципом Фермá (принципом наименьшего времени): действительный путь распространения света (траектория светового луча) есть путь, для прохождения которого свету требуется минимальное время по сравнению с любым другим мыслимым путем между теми же точками.

Рис.16. К выводу формулы линзы.

Воспользовавшись принципом наименьшего времени, рассмотрим две траектории светового луча (рис.16) – прямую, соединяющую точки А и В (луч АОВ), и траекторию, проходящую через край линзы (луч АСВ). Время прохождения света по траектории АОВ

,

где: N = n/n ₁, – относительный показатель преломления (n и n ₁, – соответственно абсолютные показатели преломления линзы и окружающей среды), с – скорость света. Время прохождения света по траектории АСВ равно

Так как t ₁ = t ₂, то

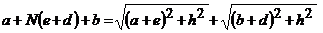(7.1)

Как и в случае преломления на сферической поверхности, используем параксиальные лучи. Тогда h << (a+e), h<< (b + d) и

.

Аналогично,

.

Подставив найденные выражения в (7.1), получим

. (7.2)

Для тонкой линзы е << a и d << b, поэтому (7.2), можно представить в виде

.

Учитывая, что

,

,

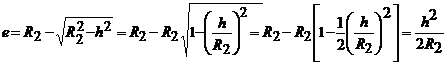получим

. (7.3)

Выражение (7.3) представляет собой формулу тонкой линзы. Отрезок а можно рассматривать, как d - расстояние от линзы до предмета, отрезок b – как расстояние от линзы до изображения (f). Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой – отрицательным. Тогда имеем

. (7.4)

Пусть лучи падают на линзу пучком параллельно главной оптической оси, т.е. из бесконечности, тогда d = ∞ (рис.17,а), тогда

(7.5)

Соответствующее этому случаю расстояние f от линзы до изображения бесконечно далекого источника называется главным фокусным расстоянием линзы и обозначается F.

Рис.17. Действие собирающей линзы.

Главное фокусное расстояние F зависит лишь от относительного показателя преломления и радиусов кривизны.

Если f = ∞ т.е изображение находится в бесконечности (рис.17,б), и, следовательно, лучи выходят из линзы параллельным пучком, то d = F. Таким образом, фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус – это точка, в которой после преломления собираются все лучи, падающие линзу параллельно главной оптической оси

Величина, D = 1/ F обратная фокусному расстоянию, называется оптической силой линзы. Ее единица – диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = 1/м.

Линзы с положительной оптической силой являются собирающими, с отрицательной – рассеивающими.

Если линзы с общей оптической осью касаются друг друга, то оптическая сила системы линзы равна алгебраической сумме оптических сил каждой из линз.

Плоскости, проходящие через фокусы линзы перпендикулярно ее главной оптической оси, называются фокальными плоскостями. В отличие от собирающей линзы рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси (рис.18).

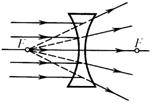
Рис.18. Действие рассеивающей линзы.

Учитывая (7.4) и (7.5), формулу линзы в общем случае можно записать в виде

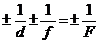. (7.6)

В формуле линзы правило знаков перед d и f аналогично таковому для формулы сферического зеркала. Перед F знак «+» ставится, когда фокус действительный (т.е. в формуле собирающей линзы); знак «–» когда фокус мнимый (т.е. в формуле рассеивающий линзы).

Формуле (7.6) в случае действительного изображения, даваемого собирающей линзой можно придать иной вид, вводя обозначение р для расстояния от предмета до переднего фокуса линза и q для расстояния от заднего фокуса до изображения:

р = d – F, q = f – F.

Подставляя величины p и q в формулу линзы (7.6), после простых преобразований получим

p q = F ². (7.7)

Такой вид соотношения для тонкой линзы называется формулой Ньютона.

Аналогия правил знаков в случаях сферического зеркала и линзы вытекает из того, что использующиеся для вывода этих формул законы отражения и преломления света подчиняются вышеупомянутому принципу Фермá (принципу наименьшего времени). Развивая эту аналогию, можно сформулировать общие правила построения изображения в сферических зеркалах и линзах. Для этой цели сферическое зеркало и линзу обозначим общим термином «система».

Построение изображения предмета в оптических системах осуществляется с помощью следующих лучей:

1) луча, проходящего через оптический центр системы и не изменяющего своего направления;

2) луча, идущего параллельно главной оптической оси; после взаимодействия с системой (преломления либо отражения) этот луч (или его продолжение) проходит через второй фокус системы;

3) луча (или его продолжения), проходящего через первый фокус системы; после взаимодействия с системой луч выходит из системы параллельно ее главной оптической оси (третий луч – луч обратный первому).

Отношение линейных размеров изображения и предмета называется линейным увеличением системы (сферического зеркала или линзы):

Если направление по световому лучу принять за положительное, то отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевернутое), положительным – мнимое изображение (оно прямое).

Освещенность изображения Е определяется отношением светового потока Ф к поверхности изображения σ, т.е. Ф/σ. При заданном расстоянии от источника до линзы световой поток, поступающий от источника через линзу к изображению, пропорционален площади линзы, т.е. пропорционален d ², где d – диаметр линзы или диафрагмы, прикрывающей линзу. Площадь изображения прямо пропорциональна квадрату расстояния изображения от линзы; если же источник находится далеко от линзы, то изображение находится вблизи фокальной плоскости и площадь изображения пропорциональна квадрату фокусного расстояния F ². Итак, освещенность изображения, даваемого линзой, пропорциональна квадрату ее диаметра и обратно пропорциональна квадрату ее фокусного расстояния (d / F)². Величина (d / F)² называется светосилой линзы. Для характеристики линзы также пользуются величиной d / F, именуемой относительным отверстием. Теоретически максимально доступная светосила объектива составляет 1:0,5.

Освещенность изображения уменьшается при ограничении светового пучка, вступающего в линзу. Но качество изображения при ограничении пучка при помощи регулируемой заслонки (диафрагмы) улучшается. Практически приходится некоторую потерю в светосиле для получения надлежащего качества изображения и, наоборот, мириться с ухудшением изображения для получения достаточной его освещенности.

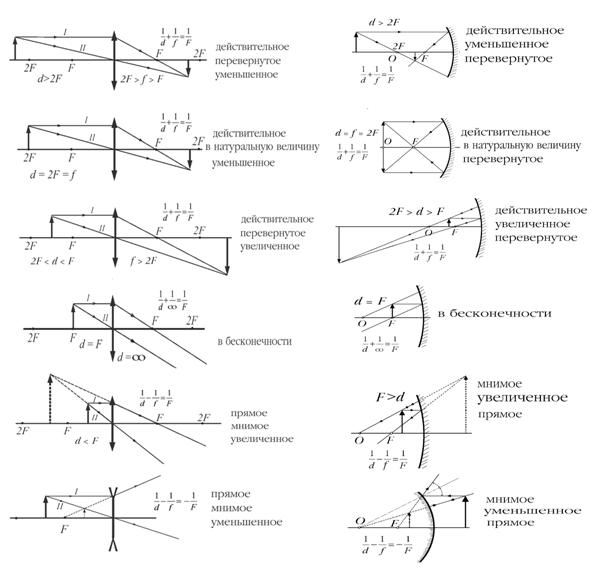
Примеры построения изображений в одиночных оптических системах характеристики изображений от предметов, находящихся на различных расстояниях d от системы и соответствующие формулы приведены на расположенном здесь рис.19.

8.Секстант

Секстант – навигационный прибор, позволяющий определять координаты судна в открытом море. Им измеряют высоту светила над горизонтом. Делается это в неблагоприятных условиях, например, на качающейся палубе, трясущимися руками и т.д.

Для объяснения ходя лучей в секстанте рассмотрим два плоских зеркала, образующих двугранный угол α рис.20.

Рис.20. Ход лучей в двугранном плоском зеркале.

На одно из зеркал падает луч, лежащий в плоскости, перпендикулярной ребру угла. Требуется определить угол отклонения луча β от первоначального направления после отражения от обоих зеркал.

Пусть угол падения луча на первое зеркало равен γ, а на второе – δ. Очевидно, что угол β как внешний угол треугольника, образованного лучами, равен 2(γ+δ). С другой стороны, γ+δ=α, потому что как угол α, так и углы γ+δ дополняют угол ω до π. Поэтому β =2α. Самое интересное, что величина этого угла не зависит от угла падения луча на зеркало! Именно это свойство и позволило использовать такую систему зеркал в секстанте. Секстантом измеряют высоту светила над горизонтом, т.е. угол β между направлениями на горизонт и на звезду (рис.21). Для этого необходимо точно зафиксировать угол α. Одно из зеркал секстанта полупрозрачное. Наблюдая сквозь него линию горизонта, изменением угла α совмещают с ней видимое в этом зеркале изображение светила. Затем величина угла α считывается со шкалы прибора.

Рис.21. Ход лучей в секстанте.

Обратим внимание на частный случай, когда зеркала образуют между собой прямой угол. Тогда β=π и падающий луч в результате двух отражений поворачивает в обратном направлении (рис.22,а). Напомним, что это справедливо только в том случае, когда падающий луч лежит в плоскости, перпендикулярной ребру двугранного угла между зеркалами.

Рис.22. Ход лучей в уголковом отражателе.

А можно ли сделать устройство, в котором падающий луч при любых условиях отражался бы назад? Оказывается, что для этого достаточно добавить к двум зеркалам третье, расположив его таким образом, чтобы плоскости всех зеркал были взаимно перпендикулярны, подобно координатным плоскостям декартовой системы (рис.22,б). При произвольной ориентации падающего луча он, испытав отражение от каждого из зеркал, будет распространятся точно в обратном направлении. Такое устройство называется уголковым отражателем или катафотом и широко применяется на практике.

Уголковые отражатели часто выполняют в виде срезанного угла стеклянного кубика, т.е. равносторонней трехгранной пирамиды. Боковые грани такого кубика делают зеркальными. Уголковые отражатели используются: зеркал в лазерных резонаторах и в дальномерах. Их преимущество в том, что они не требуют юстировки. Специальные уголковые отражатели были доставлены на Луну и использованы для точного измерения расстояния, с помощью лазерного луча. Погрешность измерения вила всего лишь 0,1 м.

Наиболее распространенное применение катафотов - это красные отражатели света, устанавливаемые на автомобилях, велосипедах и дорожных знаках. Такой отражатель представляет собой мозаику из зеркальных углов. Интересно отметить, что таким же свойством отражать падающий под любым углом свет точно в обратном направлении обладает оптический элемент, изображенный на рис.23. Он представляет собой шарик из прозрачного материала с показателем преломления п =2и с посеребренной задней поверхностью. Нетрудно показать, что луч, проходящий внутри шарика не слишком далеко от центра, после отражения на задней поверхности выйдет из шарика в обратном направлении. Это свойство используют при изготовлении светоотражающей краски для дорожных знаков; в ее состав вводят мелкие стеклянные шарики.

Рис.23. Падающий на прозрачный шарик с n =2 луч после отражения направлен точно назад.

.

9.Аберрация (погрешности) оптических систем

Рассматривая прохождение света через сферическую поверхность и тонкие линзы, мы ограничивались параксиальными лучами. Показатель преломления материала линзы считали независящим от длины волны падающего света, а падающий свет – монохроматическим. Так как в реальных оптических системах эти условия не выполняются, то в них возникают искажения изображения, называемые аберрациями (погрешностями).

1. Сферическая аберрация. Если расходящийся пучок света падает на собирающую линзу, то параксиальные лучи после преломлены пересекаются в точке S ₁ (на расстоянии OS ₁ от оптического центра линзы), а лучи, более удаленные от оптической оси – в точке S ₂, ближе к линзе, т.е ОS ₁> OS ₂ (рис.24,а). Для рассеивающей линзы, наоборот, OS ₁< OS ₂ (рис.24,б)

Рис.24. Возникновение сферической аберрации.

В результате изображение светящейся точки на экране, перпендикулярном оптической оси, будет в виде расплывчатого пятна. Этот вид погрешности, связанный со сферичностью преломляющих поверхностей, называется сферической аберрацией. Количественной мерой сферической аберрации является отрезок δ = ОS ₁– ОS ₂. Ограничиваясь параксиальными лучами при помощи диафрагмы, можно сферическую аберрацию уменьшить, однако при этом уменьшается светосила линзы. Сферическую аберрацию можно практически устранить, составляя системы из собирающих (δ <0) и рассеивающих (δ >0) линз, сферические аберрации которых взаимно компенсируют друг друга (рис.25). Сферическая аберрация является частным случаем астигматизма (см. п.5).

Рис.25.Исправление сферической аберрации путем комбинирования

собирающей и рассеивающих линз.

2. Кома. Если через оптическую систему проходит широкий пучок от светящейся точки, расположенной не на оптической оси, то получаемое изображение этой точки будет в виде освещенного пятнышка, напоминающего кометный хвост. Такая погрешность называется поэтому комой. Устранение комы производится теми же приемами, что и сферической аберрации.

Рис.26.Дисторсия изображения прямоугольной сетки

3. Дисторсия. Погрешность, при которой при больших углах падения лучей на линзу линейное увеличение для точек предмета, которые находятся на разных расстояниях от главной оптической оси, несколько различается, называется дисторсией. В результате нарушается геометрическое подобие между предметом (прямоугольная сетка, рис.26,а) и его изображением (рис.26,б – подушкообразная дисторсия, рис. 26,в – бочкообразная дисторсия).

Дисторсия особенно опасна в тех случаях, когда оптические системы применяются для съемок, например при аэрофотосьемке, в микроскопии и т.д. Дисторсию исправляют соответствующим подбором составляющих частей оптической системы.

4. Хроматическая аберрация. До сих пор мы предполагали, что коэффициенты преломления оптической системы постоянны. Однако это утверждение справедливо лишь для освещения оптической системы монохроматическим светом (λ=const); при сложном составе света необходимо учитывать зависимость коэффициента преломления вещества линзы (и окружающей среды, если это не воздух) от длины волны (явление дисперсии). При падении на оптическую систему белого света отдельные составляющие его монохроматические лучи фокусируются в разных точках (наибольшее фокусное расстояние имеют красные лучи, наименьшее – фиолетовые), поэтому изображение размыто и по краям окрашено. Это явление называется хроматической аберрацией.

Рис.27. Исправление хроматической аберрации

Так как разные сорта стекол обладают различной дисперсией, то, комбинируя собирающие и рассеивающие линзы из различных стекол, можно уменьшить расстояние между «разноцветными» фокусами. Расчет в простейшем случае ведется таким образом, чтобы фокус F _красн красных лучей и фокус F _син синих лучей попали в одну и ту же точку F (рис.27). Системы линз с устраненной таким способом хроматической аберрацией для лучей двух цветов называются ахроматами. Применяются также системы, где соединены фокусы для лучей трех цветов – апохроматы.

5. Астигматизм. Погрешность, обусловленная неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка, называется астигматизмом. Так изображение точки, удаленной от главной оптической оси, наблюдается на экране в виде расплывчатого пятна эллиптической формы. Это пятно в зависимости от расстояния экрана до оптического центра линзы вырождается либо в вертикальную, либо в горизонтальную прямую. Астигматизм исправляется путем подбора радиусов кривизны преломляющих поверхностей и их фокусных расстояний. Системы, исправленные на сферическую и хроматическую аберрации и на астигматизм называются анастигматами. Частица а перед словом означает отрицание: астигма - неточечность изображения; ана – двойное отрицание) анастигматизм – неастигматизм, т.е, точечное изображение точечного предмета.

Не нашли, что искали? Воспользуйтесь поиском: