Преломление в трехгранной призме

Рассмотрим падение луча АВ из воздуха на грань OL трехгранной призмы (рис.8), изготовленной из материала, оптически более плотного, чем окружающая среда.

Рис.8. Преломление луча света на трехгранной призме

Если бы не было призмы, луч АВ через точку В пошел бы прямолинейно. Но в точке В он испытывает преломление на границе с оптически более плотной средой, поэтому идет под углом преломления меньшим, чем угол падения (r < i). На грани OM в точке C луч снова преломляется, но на этот раз на границе с оптически менее средой, так что угол преломления больше угла падения (i ₁> r ₁). Испытав два преломления, луч оба раза отклоняется в одну сторону на суммарный угол отклонения α – угол между входящим и выходящим лучами. Грани призмы, на которых луч преломляется, называются преломляющими гранями, третья грань называется основанием. Если призма сделана из материала оптически более плотного, чем окружающая среда, то при преломлении она дважды отклоняет луч в сторону основания LM.

Найдем угол отклонения α. Угол между преломляющими гранями, называемый преломляющим углом призмы, обозначим θ. Из четырехугольника ВОСN, в котором углы при В и С прямые, найдем, что угол ВNС равен 180^o– 0. Пользуясь этим, из четырехугольника ВQСN находим

(180^o – α) + (180^o – θ) + i + i ₁, = 360^o.

Отсюда

α= i + i ₁ – θ. (5.1)

Угол θ, как внешний угол в треугольнике ВСN, равен

θ = r + r ₁, (5.2)

где r – угол преломления в точке В, а r ₁ – угол падения в точке С луча, выходящего из призмы. Далее, пользуясь законом преломления, имеем

sin i = n sin r, (5.3)

sin i ₁ = n sin r ₁. (5.4)

С помощью полученных уравнений (5.1-5.4), зная преломляющий угол призмы θ и показатель преломления n, можно при любом угле падения i вычислить угол отклонения α.

Особенно простую форму получает выражение для угла отклонения в том случае, когда преломляющий угол призмы θ мал (т.е. призма тонкая), а угол падения i невелик (тогда угол i ₁ также мал). Заменяя приближенно в формулах (3) и (4) синусы углов самими углами (в радианной мере), имеем

i = n r, i ₁ = n r ₁.

Подставляя эти выражения в формулу (5.1) и пользуясь (5.2), находим

α = n (r + r ₁) – θ = (n – 1) θ. (5.5)

Обратим внимание, что угол отклонения в призме зависит от показателя преломления вещества, из которого сделана призма.

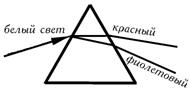
Рис.9. Разложение призмой белого света в спектр.

Показатель преломления для различных цветов света (т.е. для световой волны различной частоты) различен (дисперсия). Для прозрачных тел показатель преломления фиолетовых лучей наибольший, затем следуют лучи синие, голубые, зеленые, желтые, оранжевые, и, наконец, красные, которые имеют наименьший показатель преломления. В соответствии с этим угол отклонения α для фиолетовых лучей наибольший, для красных – наименьший, и луч белого цвета, падающий на призму, по выходе из нее оказывается разложенным на ряд цветных лучей (рис.9), т.е. образуется спектр лучей.

Не нашли, что искали? Воспользуйтесь поиском: