Вычисление основных статистических показателей

В статистике большой выборкой считается такая, в которой число наблюдений превышает 25-30. Средняя выборочная показывает средний уровень изучаемой статистической величины. При большой выборке, сведенной в ряд распределения, средняя выборочная определяется как «взвешенная» средняя арифметическая:

= (1)

где x_i – значения признака (варианта), n – объем выборки (число всех вариант), n_i – частота варианты x_i в выборке объема n, k – число различных вариант.

Выборочная дисперсия D_в и среднее квадратическое отклонение служат основными мерами вариации, рассеивания изучаемого признака вокруг его среднего значения. Выборочная дисперсия при большой выборке, сведенной в ряд распределения, вычисляется по формуле:

D_в = (2)

Размерность дисперсии равна квадрату размерности изучаемого признака, что неудобно и заставляет ввести для измерения рассеивания среднее квадратическое отклонение, имеющее размерность варьируемой величины. Его получают извлечением квадратного корня из дисперсии:

(3)

По величине среднего значения признака и величине среднего квадратического отклонения можно определить возможное наибольшее и возможное наименьшее значение признака, которые от среднего значения отличаются на тройную величину среднего квадратического отклонения (это при нормальном распределении), так как 99,7% всех единиц совокупности по величине признака от среднего его значения отклоняются не более, чем на трехкратное значение среднего квадратического отклонения (Правило «3s»).

Коэффициент вариации V является относительным показателем изменчивости и выражается в процентах:

V = 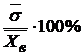(4)

Коэффициент вариации дает возможность сравнить варьирование признаков разной размерности, например, высоту и массу растений, а также используется при сравнении изменчивости величин, уровень которых резко различен, например, урожай пшеницы и корнеплодов.

Изменчивость принято считать незначительной, если коэффициент вариации не превышает 10%, средней – если коэффициент вариации выше 10%, но менее 20%, и значительной, если коэффициент вариации более 20%.

Результаты различных наблюдений, полевых и вегетативных опытов, чаще всего располагаются приблизительно в соответствии с симметричной кривой нормального распределения, когда частоты вариант, равноотстоящих от средней, равны между собой, то есть симметричны. Но нередко некоторые изучаемые признаки дают распределения, значительно отличающиеся от нормального, – асимметричные или скошенные. Для определения показателей меры косости и меры крутости кривой эмпирического распределения вычисляют коэффициенты асимметрии А и эксцесса Е соответственно. При большой выборке, сведенной в ряд распределения, вычисления ведут по формулам:

A = 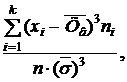(5)

E = (6)

Знак минус при А указывает на правый скос кривой распределения (вершина кривой сдвинута вправо), а знак плюс – на левый скос (вершина сдвинута влево). Знак плюс при Е указывает на повышенную крутизну кривой распределения, а знак минус – на пониженную крутизну или на наличие двухвершинности. Предельное значение Е составляет – 2: кривая распределения распалась на две самостоятельных.

Не нашли, что искали? Воспользуйтесь поиском: