Определение достоверности (надежности) выборочных статистических показателей

После вычисления того или иного статистического показателя требуется проверить степень его достоверности или надежности. Для этой цели вычисляют показатель достоверности (надежности), который представляет собой отношение величины оцениваемого статистического показателя к его ошибке:

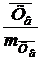t = 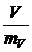; t = ; t = 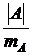; t = ; t = 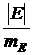. (13)

Принято оценивать достоверность статистических показателей на трех уровнях значимости: с вероятностью 95% (5%-ный уровень значимости), 99% (1%-ный уровень значимости) и 99,9% (0,1%-ный уровень значимости). В обычных исследованиях достаточно использовать 5%-ный уровень значимости. Для определения достоверности статистического показателя на заданном уровне значимости полученную величину t сравнивают со стандартной величиной t(k, ), которую определяют на нужном уровне значимости по таблице критерия t Стьюдента (Приложение 1) в зависимости от числа степеней свободы k=n-1, где n – число наблюдений (объем выборки). Если 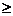t t(k, ), то значение показателя является надежным, достоверным и им можно пользоваться для различных сопоставлений и выводов. Если же t < t(k, ), то данный показатель оказывается ненадежным, величина его не достоверна и является лишь в той или иной мере вероятной.

1.4 Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона (критерию χ²)

Если по виду гистограммы, а также на основании теоретических предпосылок и анализа опытных данных мы придем к выводу, что изучаемый признак распределен по нормальному закону с плотностью:

f(x) = 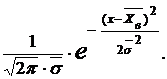(14)

где 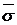– оценка среднего квадратического отклонения, – оценка математического ожидания, то выдвинутую гипотезу о нормальном распределении генеральной совокупности необходимо проверить, применив один из так называемых критериев согласия.

Критерии согласия являются объективными оценками близости фактических распределений к теоретическим. Они позволяют ответить на вопрос, вызвано ли расхождение фактического и теоретического распределения случайными величинами, связанными с недостаточным числом наблюдений, или существенными причинами, то есть тем, что теоретическое распределение плохо воспроизводит фактическое.

Рассмотрим один из критериев согласия – критерий 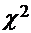, выведенный Пирсоном (английский математик 1857-1936). В нем за меру отличия эмпирической функции распределения от теоретической принимают величину

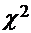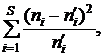= (15)

где - эмпирические частоты, 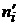- теоретические частоты, s - число интервалов выборки.

Величина 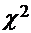является случайной и имеет, как можно показать, 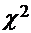–распределение. В выражении плотности вероятности этого закона распределения параметр 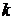назван числом степеней свободы, при этом

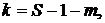(16)

где s – число интервалов выборки, 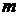- число параметров теоретического закона.

Так как нормальное распределение определяется двумя параметрами: математическим ожиданием и средним квадратическим отклонением, которые оценивались по выборке, то m = 2 и, следовательно,

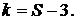(17)

При статистической проверке гипотезы задают уровень значимости 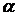, который представляет собой вероятность допустить ошибку первого рода, то есть отвергнуть правильную гипотезу. Чем меньше уровень значимости, тем меньше указанная вероятность. Обычно уровень значимости принимают равным 0,05 или 0,01. Затем, по соответствующим математико-статистическим таблицам (приложение 3) при заданном числе степеней свободы 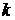и уровне значимости 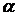находим критическую точку 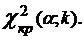Гипотеза не отвергается, если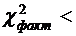 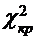, и отвергается, если > .

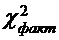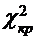Не нашли, что искали? Воспользуйтесь поиском: