Определение доверительных интервалов среднего значения, среднего квадратического отклонения и коэффициента вариации в генеральной совокупности

Статистические показатели выборочной совокупности являются приближенными оценками неизвестных параметров генеральной совокупности. Оценка может быть представлена одним числом, точкой (точечная оценка) или некоторым интервалом (интервальная оценка), в котором с определенной вероятностью может находиться искомый параметр. Так, выборочная средняя 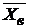является несмещенной и наиболее эффективной точечной оценкой генеральной средней , а выборочная дисперсия – несмещенной точечной оценкой генеральной дисперсии . Зная ошибку выборочной средней , точечную оценку генеральной средней можно записать в виде 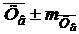. Это означает, что 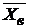– оценка генеральной средней с ошибкой, равной .

Интервальной называют оценку, которая характеризуется двумя числами – концами интервала, покрывающего оцениваемый параметр. Доверительным называют такой интервал, который с заданной вероятностью покрывает оцениваемый параметр. Центр такого интервала – выборочная точечная оценка, а пределы интервала или доверительные границы определяются средней ошибкой оценки и уровнем доверительной вероятности. Таким образом, интервальная оценка является дальнейшим развитием точечной оценки, которая при малом объеме выборки неэффективна. В общем виде, доверительный интервал для генеральной средней записывают так:

(18)

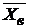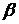где – генеральная средняя, – выборочная средняя, – ошибка выборочной средней, – значение критерия Стьюдента, где – число степеней свободы, – уровень значимости, , – доверительная вероятность или надежность.

Аналогично строится доверительный интервал для коэффициента вариации в генеральной совокупности:

(19)

где – коэффициент вариации генеральной совокупности, – коэффициент вариации выборочной совокупности, – ошибка коэффициента вариации, – значение критерия Стьюдента.

Для нахождения доверительного интервала для среднего квадратического отклонения в генеральной совокупности по найденному выборочному значению 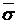используем формулу:

(20)

Для определения необходимо воспользоваться таблицей (Приложение 2).

2. ЗАДАНИЕ К РАСЧЁТно – графической работе

Не нашли, что искали? Воспользуйтесь поиском: