Умножение и деление на 10, 100, 1000

В концентре 1000 были рассмотрены случаи умножения на 10 и 100. Это же правило распространяется и на умножение, и на деление многозначных чисел на 10 и 100.

Однако первоначально следует повторить с учащимися те слу­чаи умножения 1000 на однозначное число, которые они рассмат­ривали еще при изучении нумерации:

1000 х 2= 1000+1000=2000 или

1 тыс. х 2=2 тыс.=2000 1000x5=1 тыс. х 5=5 тыс.=5000

Рассматривается еще несколько случаев умножения 1000 на числа. После этого учащиеся, сравнивая произведение, множите­ли, смогут самостоятельно сделать вывод:

Если один множитель — число 1000, то в произведении ко второму множителю надо приписать три нуля.

Используя знание переместительного закона умножения, уча­щиеся смогут решить примеры вида 3x1000.

Деление на 1000, так же как и деление на 10, 100, как пока­зывает опыт, лучше усваивается как деление по содержанию. Поэтому сначала решается задача: «Нарубили 8000 кг капусты. Для хранения ее нужно разложить в чаны. В каждый чан войдет по 1000 кг капусты. Сколько потребуется чанов?» Решение. 8000 кг: 1000 кг. Если 8 тыс. разделить по 1 тыс. (8 тыс.:1 тыс.), то получим 8. 8000 кг: 1000 кг=8 (чанов).

Рассматривается еще несколько аналогичных примеров. В ре­зультате учащиеся делают вывод по аналогии с делением на 10 и 100.

Если делитель равен тысяче, то в делимом надо отбросить три нуля и полученное число записать в частное.

Примеры на деление на 10, 100, 1000 записывается в строчку (42 000:1000=42) и решаются устно. Решаются примеры на деле­ние как без остатка, так и с остатком:

80: 10=8 800: 100=8

8000: 1000=8

85: 10=8 (ост. 5) 807: 100=8 (ост. 7)

8507: 1000=8 (ост. 507) 870: 100=8 (ост. 70)

Учитель постоянно должен напоминать учащимся, что остаток должен быть меньше делителя. Действие деления как без остатка, так и с остатком учащиеся должны учиться проверять. Например:

3800:100=38.

Проверка. 38x100=3800. 7518:1000=7 (ост. 518). Проверка. 7x1000+518=7518.

Познакомившись с умножением и делением на единицу с нуля­ми, учащиеся с трудом дифференцируют правила умножения и деления на 10, 100, 1000, смешивают эти правила, не могут вспомнить, когда нужно нули приписывать, а когда их отбрасы­вать. Это происходит особенно часто при умножении в случае, когда в первом множителе есть нули. Например: 3800x10. В произведении ученик может написать число 380. При делении

3856:10 в частное ученик переписывает делимое и нуль справа, т. е. получает 38 560.

Такие ошибки возникают, как правило, при самостоятельном выполнении действий, когда некому наводящим вопросом актуали­зировать вовремя имеющиеся знания, направить внимание учени­ка на анализ выполняемой операции с числами.

Предупреждению возможных ошибок и лучшей дифференциа­ции действий умножения и деления на 10, 100, 1000 служит чередование примеров на умножение и деление, их сопоставле­ние, сравнение ответов (при умножении число увеличивается, при делении уменьшается), способов выполнения действий, а также решение сложных примеров, в которых имеются оба действия: 4700:100x1000.

Умножение и деление на разрядные числа (десятки, сотни, тысячи)

Умножение на разрядные числа. Подготовительным упражне­нием к умножению на разрядные числа является повторение таб­личного умножения, умножения на однозначное число, а также на 10, 100, 1000. Следует вспомнить, как круглое число представить в виде произведения двух чисел (например, 20=2-10, 500=5-100, 6000=6-1000), повторить уже известные учащимся случаи умножения на круглые числа (например,

24 12 • 20=12 - (2 -10)=(12 • 2) -10=24 -10=240), вспомнить

30 правило: чтобы умножить число на круглые десятки,

720 нужно умножить это число на число десятков и к полу­ченному произведению приписать нуль, т. е. умножить его на 10.

Это правило учащиеся применяют и при умножении больших чисел в пределах 10 000, 100 000 и 1 000 000. Аналогично учащиеся знакомятся с умножением двузначных, трех- и четырехзначных чисел на круглые сотни: 25 - 300=25 • 3 -100=75 • 100=7500.

На умножение на круглые тысячи распространяется уже из­вестное учащимся правило умножения числа на круглые десятки и сотни.

Сначала рассматривается устно решение примеров вида: 7x5000. Можно 5000 записать как произведение 5-1000. 7 - (5 -1000)=(7 • 5) -1000=35 -1000=35 000.

Деление на разрядные числа. Учащиеся уже знакомы с деле­нием на круглые десятки и сотни. При изучении действий в

пределах 1000 они опираются на этот знакомый материал. Поэто­му необходимо повторить табличное деление, деление на 10, 100, 1000 и, так же как в умножении, вспомнить, как представить круглые числа в виде произведения двух чисел (30=3-10, 300=3-100, 3000=3-1000), повторить устные и письменные слу­чаи деления.

Деление на круглые сотни, а затем и тысячи можно показать на устных случаях деления, основываясь на приеме последова­тельного деления:

2500:500=2500:100: 5=25: 5=5;

250 000:5000=250 000:1000:5=250:5 = 50.

Затем вводится деление на круглые десятки, сотни и тысячи с остатком. Например: 670:40. В частном будет двузначное число. В частном берем по 1, умножаем 1 на 40. Вычитаем 67—40=27. 270 делим на 40. Сначала делим 270 и 40 на 10. Затем делим неполное делимое и делитель: 27:4. Берем по 6. Умножаем 6 на 40, получаем 240. Вычитаем. Остаток 30 (меньше 40), частное 16.

Наряду с общими случаями учащиеся разбирают решение осо­бых случаев, когда в частном получаются нули:

Умножение на двузначное число

При умножении на двузначное число до сознания школьников необходимо довести тот факт, что первый множитель умножается дважды: сначала на единицы множителя, а затем на десятки мно­жителя. Это не сразу понимают все ученики, а поэтому и закан­чивают умножение раньше, считая, что они все сделали, найдя первое промежуточное произведение. Многие учащиеся вспомога­тельной школы не осознают необходимости сложения двух про­межуточных произведений.

Все это требует от учителя школы VIII вида тщательного, неторопливого объяснения, а от учащихся — подробных рассуж­дений, комментирования выполняемых действий.

Рассуждения можно провести так: 246 -132. Множитель — дву­значное число. Оно состоит из 2 ед. и 3 дес. Сначала первый множитель 246 умножим на 2 ед. Затем 246 умножим на 3 дес., или 30.

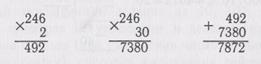
К первому произведению прибавим второе. Мы произвели три действия:

1) умножили 246 на единицы множителя;

2) умножили 246 на десятки множителя;

3) сложили полученные произведения.

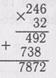
Для удобства записи и более быстрого умножения на двузнач­ное число запись и вычисления производят так: множители запи­сывают друг под другом, проводят черту и ставят знак умножения слева. Умножают первый множитель на единицы второго и запи­сывают полученное произведение под чертой. Это первое непол­ное произведение. Умножение еще не закончено, первый множитель умножают на десятки второго и первое число, полученное от умножения на десятки, записыва­ют под десятками (6 умножили на 3 десядка, получили 18 десятков). Умножили все число на десятки и получи­ли второе неполное произведение. Теперь между первым и вторым произведениями ставим знак «плюс» и склады­ваем их. Число, полученное в ответе (7872), — произведение от умножения двух чисел (246 и 32).

Ученики так же подробно объясняют решение первых приме­ров. Затем для выработки навыков вычислений объяснения свер­тываются. Однако время от времени учитель возвращается к ним. Полезно сопоставить пример на умножение на двузначное число с примером на умножение на круглые десятки, установив, что общего и что различного в их решении. Например:

Необходимо рассмотреть случаи умножения на двузначное число, когда первый множитель оканчивается нулем (540x37). Чтобы умножить 540 на 37, надо 54 десятка умножить на 37, получим 1998 десятков. К полученному произведению припишем нуль, т. е. умножим его на 10.

Учитель может и не выделять как особые случаи умножение на круглые десятки или умножение чисел, оканчивающихся нулями, не изменяя при этом привычную для учащихся форму записи и алгоритм вычисления, например:

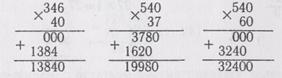
От такой развернутой формы записи можно отказаться посте­пенно, подождав момента, когда учащиеся сами поймут, что при умножении на нуль неполное произведение всегда равно нулю и его можно не записывать.

Деление на двузначное число

Деление на двузначное число впервые вводится в 7-м классе школы VIII вида. Первое знакомство с этим видом деления проис­ходит на примерах внетабличного деления, а именно при делении двузначного числа на двузначное, когда в частном получается однозначное число. В этом случае частное отыскивается приемом округления делимого и делителя до круглых чисел. Например: «При отыскании частного 93:31 округляем делимое 93 до 90, делитель 31 до 30. Тогда 90:30=3. Значит, в частном надо взять по 3. Проверяем: 31x3=93. Ответ верен.

Рассмотрим другой пример: 81:27. Округлим 81 до 80, а 27 до 30, получим 80:30. Можно взять по 2. Проверим: 27x2 = 54, 84—54=27. Значит, в частном должно быть большее число. Берем по 3. Проверяем: 27x3=81. Частное равно 3».

Однако, как показывает опыт, такие рассуждения и множество промежуточных вычислений доступны не всем учащимся. Поэтому целесообразно учащихся познакомить с приемом деления, который доступен большинству умственно отсталых школьников, если они овладели приемом умножения двузначного числа на однозначное. Учитель показывает, что при делении на двузначное число труд­нее всего правильно подобрать цифру частного. Чтобы преодолеть эту трудность можно воспользоваться последовательным умноже-

нием частного на числа 1, 2, 3 и т. д., пока не получится число, близкое к делимому. Например, 81:27.

27x1 —27 — это число меньше 81.

27x2=54 — это число меньше 81.

27x3 = 81 — получилось число, равное делимому, значит, надо в частном взять по 3. Все промежуточные действия умножения для отыскания нужной цифры частного необходимо производить в тетради. Запись решения примера выглядит так:

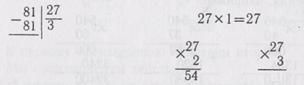
Далее последовательно рассматривается деление трех-, четы­рех-, пяти- и шестизначных чисел на двузначное число.

При решении всех этих примеров необходимо учитывать, что отделяемые две цифры делимого составляют число, которое либо равно, либо больше делителя, и только после этого рассматрива­ются случаи, когда это число меньше делителя, и в этих случаях требуется отделить три цифры делимого.

Наиболее успевающие по математике учащиеся постепенно со­кращают число проб на умножение; умножение делителя на 1 они не записывают, некоторые устно умножают делитель на 2, а то и на 3, и начинают умножать на 4 и 5 и т. д.

Естественно, что сильным учащимся следует показать прием округления делимого и делителя.

Например, рассматривается деление трехзначных чисел на дву­значное число при однозначном частном и, например: 465:93. Рассуждения проводим так: «Делитель заменяем круглым числом. Это число 90, или 9 десятков. В делимом тоже отделяем десятки, их 46. Делим 46 на 9. В частном берем 5. Проверяем, умножая 93x5. В данном случае 5 подходит».

Рассматриваются и случаи деления с остатком:

35 ТГост. 28)

Вслед за делением с остатком рассматривается деление трех­значного числа на двузначное, когда в частном получается дву­значное число. Вначале в делимом подбираются такие числа, в которых первое неполное делимое состояло бы из двух цифр, а делитель состоял из цифр, не превышающих 5. «При выполнении деления делитель заменяем наименьшим круглым числом 20. В делимом отделяем две цифры. Первое неполное делимое — 80 десятков. В частном будет двузначное число. 80 делим на 20, будет по 4, но по четыре брать нельзя, так как 23x4=92. Берем по 3. Проверяем: 23x3=69, 80—69=11. Остаток меньше делите­ля. Значит, первую цифру подобрали правильно. 115 делим на 20. Берем первые две цифры делимо­го (11) и первую цифру делителя (2), 11 делим на 2. Берем по 5. Проверяем: 23x5=115. Вычитаем. Остатка нет. Значит, 5 подобрали правильно. Частное 35. Проверим умножением: 35x23 = 805». После этого рассматриваются случаи деления четырехзначного числа на двузначное.

И наконец, рассматриваются такие случаи деления: число, со­стоящее из двух цифр делимого, не делится на делитель.

Рассуждения проводятся так: «17 тысяч не де­лятся на 43, тогда на 43 разделим 178 сотен. В частном получится трехзначное число — ставим 3 точки. Делитель 43 заменим меньшим круглым числом 40. Делим 178 на 40. Берем в делимом первые две цифры, а в делителе первую цифру. Получаем делимое 17, а делитель 4. 17 делим на 4. Берем по 4, проверяем умножением и т. д.».

В методической литературе, связанной с вопросами начального обучения математике, после окончания деления ставится нуль, показывающий, что деление закончено и произведено без остатка.

В школе VIII вида нуль записывать не рекомендуется. Опыт показывает, что учащиеся (по аналогии с решением примеров, в которых нули переносятся в частное из делимого) этот нуль сно­сят в частное, рассуждая при этом так: «О делим на 82, получает­ся нуль. В частное записываем нуль».

Особое внимание необходимо уделять рассмотрению случаев, когда делимое оканчивается нуля­ми и когда нули получаются в середине частного. Подготовительными упражнениями являются деление нуля (0:5, 0:12), а также решение при­меров с небольшими числами вида 320:8=40, 312:3 и т. д. Рассмотрим решение примера 24 000:75. Рассуждения проводятся так:

«Первое неполное делимое — 240 сотен. Зна­чит, в частном будет трехзначное число. Ставим 3 точки. Округляем делитель до 70. Делим 240 на 75 70. Сначала 24 делим на 7. Берем по 3. Проверяем умножением. Остаток 15. Делим 150 дес. на' 75. 15:7 берем по 2. Проверяем умножением. Де­сятки разделились все. Делим 0 единиц: 0:75=0. Пишем в частном 0. Частное 320»: После изучения всех четырех арифметических действий для закрепления вычислительных навыков решаются примеры вида 626 640:84+212 760x36, (7368+28 300)х 12-17 899.

Вопросы и задания

1. Составьте схему последовательности изучения нумерации многознач­
ных чисел по I и II вариантам.

2. Изготовьте эскизы таблиц для изучения нумерации многозначных
чисел, покажите методику их использования.

3. Сравните алгоритмы умножения (деления) многозначного числа на
однозначное, двузначное, трехзначное числа.

4. Проанализируйте ошибки учащихся при выполнении четырех арифме­
тических действий, определите их причины, наметьте пути преодоления.

Глава 14

МЕТОДИКА ИЗУЧЕНИЯ МЕТРИЧЕСКОЙ СИСТЕМЫ МЕР

Не нашли, что искали? Воспользуйтесь поиском: