Умножение и деление на однозначное число с переходом через разряд.

Этот вид умножения и деления представляет наибольшие труд­ности для учащихся. Умножение и деление с переходом через разряд выполняется приемами письменных вычислений. Учащиеся при этом впервые знакомятся с алгоритмом письменного умноже­ния и деления. Поэтому, так же как при сложении и вычитании, следует познакомить учащихся с записью действий в столбик на самых легких случаях умножения (нет перехода через разряд) и деления (каждый разряд делимого без остатка делится на дели-

тель). Затем следует расположить материал по нарастающей сте­пени трудности в такой последовательности:

Умножение

1. Умножение двузначного числа на однозначное с переходом
через разряд в разряде десятков или единиц (27x3, 74x2).

2. Умножение двузначного числа на однозначное с переходом
через разряд в разряде единиц и десятков (85x3).

3. Умножение трехзначного числа на однозначное с переходом
через разряд в одном разряде — единиц или десятков (127x3,
154x2).

4. Умножение трехзначного числа на однозначное с переходом
через разряд в двух разрядах — единиц и десятков (175x3).

5. Особые случаи умножения — первый множитель — трех­
значное число с нулем на конце или в середине (280x3, 208x3).

6. Умножение двузначного числа на круглые десятки (27x20).
Знакомство с новой записью умножения в столбик, как уже

было сказано выше, целесообразно показать на самых легких при­мерах, в которых сам процесс вычислений не представляет для учащихся никаких трудностей и все внимание должно быть сосре­доточено на новой форме записи примера, например: 123x3. Сна­чала учащимся предлагается решить этот пример устно. Затем учитель знакомит учащихся с записью этого примера в столбик и его решением. Рассуждение проводится так: «Запишем первый множитель 123. Второй множитель — однозначное число, которое состоит из единиц, поэтому множитель подписываем под единица­ми первого множителя. Проводим черту, слева ставим знак умно­жения и начинаем умножать с единиц. 3 единицы умножим на 3, получим 9 единиц; подписываем их под единицами. Умножим 2 десятка на 3, получим 6 десятков; подпишем их под десятками. Умножаем сотни, 1 сотню умножим на 3, получим 3 сотни; подпи­сываем 3 сотни под сотнями. Произведение равно 369».

Решается несколько аналогичных примеров. Особое внимание учащихся надо обратить на последовательность умножения и пра­вильность записи произведения. Нужно помнить о том, что по аналогии с устными приемами вычислений учащиеся начинают умножение не с единиц, а с сотен, а результат умножения подпи­сывают под единицами. Поэтому на первых порах запись множи­телей и произведения целесообразно давать в три цвета (едини­цы — одним цветом, десятки — другим, сотни —третьим).

При решении примеров на умножение с переходом через раз­ряд трудность вызывает не только запись примеров, но и сам процесс вычислений. Учащиеся забывают прибавить число, кото­рое они держали в уме, забывают, сколько надо прибавить. В этом случае учащимся можно разрешить записывать числа, кото­рые нужно запомнить, на отдельном листочке — черновике (он должен быть в тетради каждого ученика класса).

Особое внимание нужно уделить решению примеров с перехо­дом через разряд в двух разрядах.

Эти примеры наиболее трудны, поэтому их необходимо решать больше.

Умножение трехзначных чисел с нулем на конце или в середи­не требует особо пристального внимания, так как учащихся за­трудняет умножение нуля: они путают его со сложением с нулем. Поэтому предварительно надо повторить умножение нуля и на нуль (0x3, 5x0).

При умножении чисел, оканчивающихся нулем, учитель вспо­могательной школы использует различные формы записи. В одних случаях множитель подписывается под нулем, в других — под первой значащей цифрой:

При первой форме записи рассуждения проводятся так: «О единиц умножаем на 3, получается 0, подписываем 0 под еди­ницами. 8 десятков умножаем на 3, получаем 24 десятка. 4 десят­ка записываем под десятками, а 2 сотни запоминаем. 2 сотни умножаем на 3, получаем 6 сотен, прибавляем к ним 2 сотни, получаем 8 сотен, 8 сотен подписываем под сотнями. Произведе­ние равно 840».

При второй форме записи рассуждения проводятся так: «В числе 280 содержится 0 единиц; при умножении 0 на любое число получается 0, поэтому начинаем умножать сразу десятки; 8 десят­ков умножаем на 3, получаем 24 десятка. 4 десятка записываем под десятками, а 2 сотни запоминаем, 2 сотни умножаем на 3, получаем 6 сотен, прибавляем еще 2 сотни, получаем 8 сотен, 8

сотен записываем под сотнями. О единиц сносим. Произведение равно 840».

При второй форме записи нужно время от времени спрашивать учащихся, почему нуль сносится в произведение. В противном случае учащиеся делают эту операцию механически.

Учащихся следует познакомить только с одной формой записи.

Умножение на круглые десятки

В пределах 1000 рассматриваются случаи умножения двузнач­ных чисел на круглые десятки. Учитывая то, что учащиеся уже знакомы с приемами письменных вычислений, умножение на круг­лые десятки выполняется письменно. Это облегчает процесс вы­числения. Запись умножения двузначного числа на двузначное число надо объяснить подробно, показав аналогию с записью чисел в столбик при сложении и вычитании (единицы и десятки

множителей подписываются соответственно друг под дру-

гом, и умножение начинается с единиц).

д_ля слабоуспевающих по математике учащихся эта за-

пись может оставаться единственной. Остальных учащих-— FjTT ся по усмотрению учителя можно познакомить с более

свернутой формой записи примеров такого вида, при кото-

рой умножение на нуль не производят, например 27 • 20:

т. е. нуль второго множителя не подписывается под значащей цифрой. Производится умножение первого множителя на два, т. е. на число круглых десятков, а потом полученное произведение умножается на 10, т. е. приписывается к нему нуль справа.

Такая операция может быть понятна учащимся только в том случае, если будет проведена подготовительная работа. Перед ум­ножением на круглые десятки устно следует повторить случаи вида 2x2x10, 2x20 и сравнить ответы этих примеров, объяс­нить, почему произведения равны. Учащиеся убеждаются, что вто­рой множитель — круглый десяток (20, 30,..., 90) — можно разложить на два множителя: на число десятков и 10. Сначала умножаем множитель на число десятков, а потом на 10. Затем надо порешать примеры на умножение двузначного числа на 10 (27x10, 38x10 и т. д.).

Решать примеры вида 27x20 следует устно. Объяснение их надо давать так, чтобы учащиеся поняли, почему умножаем на число десятков, а нуль приписываем к полученному произведению справа. Рассуждения проводятся так: «20 можно записать как произведение, т. е. 20=2x10, 27 -20=27. 2- 10=54- 10=540».

Запишем решение этого примера в столбик:

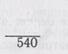
х²⁷

^Х 20

Сначала 27 умножим на 2, получим 54, а потом произведение 54 умножим на 10, т. е. припишем к нему 0 справа.

На первых порах учащиеся при решении этих примеров долж­ны давать подробные объяснения. Затем рассуждения постепенно свертываются, но иногда следует задавать учащимся вопросы: «Почему при умножении на круглые десятки приписываем 0 спра­ва? В виде произведения каких двух чисел можно записать второй множитель? На какое число сначала умножали первый множи­тель? На какое число потом умножали полученное произведе­ние?» Эти вопросы позволяют учащимся более сознательно подхо­дить к процессу выполнения умножения на круглые десятки. Кроме того, они готовят почву для сознательного выполнения умножения чисел на круглые сотни и тысячи.

Деление

Деление изучается в такой последовательности:

1) число сотен, десятков и единиц делится без остатка на
делитель (369:3);

2) число сотен делится на делитель без остатка, а число десят­
ков без остатка на.делитель не делится (372:3);

3) число сотен не делится без остатка на делитель (570:3);

4) число сотен делимого меньше числа единиц делителя, в
частном получается двузначное число (153:3);

5) особые случаи деления, когда в частном на конце или в
середине получается нуль (720:3, 812:4, 820:4);

6) деление на круглые десятки.

Деление трехзначного числа на однозначное, когда сотни, де­сятки и единицы нацело делятся на делитель, учащиеся выполня­ют устно: 369:3 = 123. Однако на примере такого вида следует познакомить учащихся с новой формой записи деления в столбик. Рассуждения проводятся так: «Сначала записываем делимое. Знак деления обозначаем прямым углом, одна из сторон которого не-

сколько продолжена вниз. Внутри угла записываем делитель. Деление начинаем с сотен (с высшего раз­ряда). Частное от деления каждого разряда записыва­ем под делителем. 3 сотни делим на 3, получаем 1 сотню, записываем ее в частное. Проверяем, все ли сотни разделили. 1 сотню умножаем на 3 и пишем под сотнями. Ставим знак «минус» (сотни вычитаем). Сносим 6 десятков и делим их на 3. И т. д. Частное 123».

Действие деления наиболее трудно для учащихся. Особенно труд­ны те случаи деления, в которых один или два разряда нацело не делятся на делитель, или случаи, в которых в частном получается нуль в середине. Умственно отсталые школьники допускают нередко ошибки, связанные с неправильным подбором числа в частном, — их не смущает, что при вычитании в остатке получается число, делящееся на делитель или больше делителя. Учащихся не смущает и то, что число, получившееся в частном, больше делимого.

Нередко в частном получается число, имеющее большее число знаков, чем делимое. Причинами таких ошибок опять являются неправильный выбор частного, получающийся больше делимого (или равный делителю) остаток. Например:

Для того чтобы предотвратить подобные ошибки в вычислени­ях и помочь учащимся овладеть трудным для них действием деле­ния, необходимо задолго до знакомства с приемами письменного деления провести подготовительную работу:

1. Постоянно, на каждом уроке повторять таблицу умножения
и деления.

2. Решать примеры на деление с остатком: 15:2=7 (ост. 1);
21:4=5 (ост. 1); 61:6=; 82:2= и т. д., обращая внимание на
то, что остаток должен быть всегда меньше делителя. Подбор
цифр частного, например 24:5, следует производить постепенно:
24 на 5 не делится, делим 23, потом 22, 21, наконец, 20.

С самого начала знакомства с делением в столбик надо учить детей прикидке ответа, умению сразу определять, сколько цифр должно получиться в ответе.

Например, если делится трехзначное число на однозначное, а число сотен делимого больше делителя или равно ему, то в част­ном получатся сотни. Сотни стоят в числе на третьем месте. Значит, в ответе должно получиться трехзначное число. Можно рекомендовать в частном поставить сразу три точки, например:

Если в трехзначном числе число сотен меньше делителя, то сотни надо раздробить в десятки, прибавить десятки делимого и начинать деление. В этом случае в частном получится двузначное число, так как десятки стоят на втором месте. В частном 148|3 учащиеся ставят две точки. Предварительная прикидка количест­ва цифр в числе предотвращает возможность пропуска нуля в частном или его недописывание. Особое внимание уделяется ре­шению примеров, когда среди цифр частного получается нуль:

~ О

~ 16

Когда учащиеся усвоят алгоритм деления, можно познакомить их с сокращенной записью.

2161 2 108

Действие деления проверяется умножением. Решаются сложные примеры на все четыре арифметических действия и на порядок действий.

Деление на круглые десятки

Предварительным материалом к данной теме является решение примеров вида 80:20, 120:20, в которых учащиеся деление произ­водят как деление по содержанию 8 дес.:2 дес.=4 (раза), 12 дес.:2 дес.=6. На основании решения таких примеров учащие-210

ся убеждаются, что если делимое и делитель оканчиваются нуля­ми, то частное легче получить, если деление выполнять, не обра­щая внимания на нули, т. е. мысленно отбросить (120:20=6). При этом обращается внимание учащихся на то, что, отбрасывая нуль в делимом, мы его делим на 10.

Затем учащиеся знакомятся с делением трехзначно­го числа на двузначное, используя алгоритм письмен-

24" ного деления: делим 72 десятка на 3 десятка. От уча­щихся необходимо требовать проверки действия деле-

__________ ния умножением.

Для закрепления действий, выработки прочных на­выков вычислений и повторения теоретических знаний решаются примеры на нахождение неизвестных компонентов дей­ствия, порядок действий.

Вопросы и задания

1. Подготовьте сообщение на тему «Особенности и трудности усвоения
нумерации многозначных чисел».

2. Составьте схему последовательности изучения нумерации первой тыся­
чи.

3. Составьте фрагмент урока на одну из тем: «Нумерация круглых сотен»,
«Устная нумерация трехзначных чисел», «Письменная нумерация трехзнач­
ных чисел». Изготовьте наглядные пособия к этим урокам.

4. Составьте примеры на сложение и вычитание с возрастающей степе­
нью трудности.

5. Какие трудности испытывают учащиеся при решении примеров вида
814—208, 346—149? Каковы пути преодоления этих трудностей?

6. Раскройте систему и методику ознакомления с алгоритмами письмен­
ного умножения и деления.

Не нашли, что искали? Воспользуйтесь поиском: