ТАБЛИЧНОЕ ДЕЛЕНИЕ В ПРЕДЕЛАХ 100

Составлению таблиц деления в пределах 100 предшествует повторение таблиц деления в пределах 20, сопоставлению табли­цы умножения и соответствующей таблицы деления. Учащиеся наблюдают взаимную связь этих арифметических действий. Уча­щиеся уже могут по примеру на умножение составить два приме­ра на деление: 3x4=12; 12:3=4, 12:4=3 в пределах 20.

Последующие таблицы деления составляются уже с опорой на установленную взаимосвязь между действиями умножения и деле­ния. Только для отдельных учащихся, наиболее отсталых в умст­венном развитии, приходится использовать прием деления пред­метных совокупностей на равные части и в дальнейшем.

На основании установления взаимосвязи между умножением и делением учитель знакомит учащихся с проверкой деления умно­жением. Учащиеся практически, без заучивания правил, должны понять, что деление можно проверить умножением так: деление выполнено правильно, если при умножении частного на делитель в ответе получится делимое.

Например: 15:3=5, 5x3=15.

Пониманию взаимосвязи между умножением и делением спо­собствует решение и составление пар, а также четверок примеров такого вида:

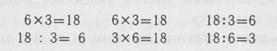
В школе VIII вида, несмотря на проводимую работу по установ­лению взаимосвязи между действиями умножения и деления, не­которые умственно отсталые школьники так и не осмысливают эту связь глубоко, а поэтому решают и даже составляют пары и четверки примеров механически. Все это приводит к необходимос­ти заучивать не только таблицу умножения, но и таблицу деле­ния.

Установка на запоминание должна быть дана учащимся сразу. Для лучшего запоминания таблицы учащимся нужно постоянно показывать, как составляются примеры одной таблицы, какая тут закономерность: таблица умножения составляется по постоянному первому множителю, второй множитель увеличивается в каждой последующей строчке на 1, произведение увеличивается на число единиц первого множителя. Полезно предлагать учащимся зада­ния на составление следующего или предыдущего примеров из таблицы: 5-4=20, составить следующий пример: 5-5=25; срав­нить эти примеры. Вопросы могут быть следующими: на какое число отличаются произведения и почему? Какой ответ у предыду­щего примера?

Аналогичные таблички учащиеся должны изготовить на уроке труда из плотной бумаги. Эти таблички с названием всех компо­нентов и результатов действий учащиеся хранят в тетрадях по математике и постоянно с ними работают.

Задания могут быть такого типа: по примеру на умножение составить один пример на деление, по примеру на умножение составить один пример на умножение и два примера на деление:

Аналогичные таблички учащиеся должны изготовить на уроке труда из плотной бумаги. Эти таблички с названием всех компонентов и результатов действий учащиеся хранят в тетра­дях по математике и постоянно с ними работают. Полезны упражнения:

2. В примере 40: 5=8 назвать делимое, частное, делитель. В
примере 3x6=18 назвать множители, произведение.

3. Делимое 32, делитель 4. Найти частное. Сомножители 3 и 9.
Найти произведение.

4. Найти частное двух чисел: 12 и 6.

5. Что неизвестно в примерах на деление:

6. Заполнить пустую клетку в примере нужным чис­
лом.

Умножение 1 на 1 и деление на 1 выделяются особо в программе, так как эти случаи не вытекают из определения умно­жения. С этими случаями умножения и деления учащиеся знако­мятся после изучения всей таблицы умножения и деления.

По возможности знакомство с этими особыми случаями умно­жения надо провести наглядно, не ограничиваясь просто заучива­нием правил.

В работе с единицей рассматриваются два случая.

Умножение по 1. Этот вид умножения лучше начинать с умно­жения I на большие числа, например: 1x6 — это 1 + 1 + 1 + 1 + 1 + 1=6, 1 + 1 + 1 + 1 + 1 = 1x5, 1X2=2. Если 1 умно­жить на число, то получится это же число. Этот вывод можно сделать и на основе решения задачи жизненно-практического со­держания. Например, учитель говорит и показывает: «По 1 каран­дашу взяли 4 ученика. Сколько карандашей они взяли?»

Умножение на 1. Это особый случай умножения. Учитель сообщает, что 5 • I нельзя рассматривать как сумму одинаковых слагаемых, так как тут нет слагаемых. Используем переместитель-ное свойство умножения: если 1-5=5, то 5-1=5.

Учащиеся заучивают правило:

Если один из множителей единица, то произ­ведение равно второму множителю.

Деление на 1 рассматривается на основе знания взаимоотноше­ния между умножением и делением: 1-3=3, следовательно 3:1=3.

Показ деления на конкретных примерах лучше усваивается ребятами, например: «3 конфеты разделить на один (1), значит, дать их одному человеку. Сколько конфет получит этот человек?»

Необходимо сопоставлять решение примеров вида

Умножение нуля, умножение на нуль и деление нуля. На

основе знания смысла умножения как сложения равных слагае­мых можно записать: 0x5=0+0+0+0+0=0, значит, 0x5=0.

При умножении числа на 0 следует сделать ту же оговорку, что и при умножении числа на единицу. Даем правило: при умно­жении любого числа на 0 произведение равно 0. Далее показыва­ем, что переместительное свойство умножения здесь можно при­менить так: если 5x0=0, а 0x5=0, то 5x0=0x5.

Учащимся предлагается заучить правило:

Если один из множителей нуль, то произведе­ние равно нулю (0).

Деление нуля рассматривается на основе взаимосвязи умноже­ния и деления: 0x3=0, отсюда 0:3=0.

Однако понятнее для учащихся оказывается ссылка на опреде­ленную жизненную ситуацию: «У меня нет ни одной конфеты, т. е. нуль конфет; я буду делить нуль на трех человек. Сколько конфет получит каждый?» Такие примеры сразу дают учащимся возможность осознать, что при делении нуля на любое число в частном получается нуль.

Невозможность деления на нуль дается на основе правила.

В примерах, где компонентами действий является 0 или 1, уча­щиеся допускают много ошибок. Поэтому полезны упражнения, спо­собствующие дифференциации этих понятий. Это примеры вида

Деление по содержанию в школе VIII вида рассматривается лишь при решении арифметических задач после изучения таблицы умножения и деления на равные части. Примеров на деление по содержанию не дается.

Деление с остатком вводится после изучения табличного де­ления (4-й класс). На деление с остатком дети допускают много ошибок. Они либо не записывают остаток (8:3=2), либо прибав­ляют его к частному (8:3=4 — к частному прибавили остаток 2), либо получают остаток больше делителя (8:3=1) (ост. 5).

Перед решением примеров на деление с остатком полезно, как показывает опыт, выполнять подготовительные упражнения: 3x4+1. Понятие о делении с остатком необходимо дать путем создания определенной жизненной ситуации, в которой учащиеся убеждаются, что нередко при делении получается остаток. Напри­мер, учитель вызывает двух учеников, а третьего просит разде­лить между двумя учениками поровну сначала 2 тетради, потом 3, 4, 5 тетрадей. Деление конкретных предметов сопровождается записью примеров и комментированием: 2:2 = 1, 3 разделить на две равные части (каждый ученик получил по одной тетради, и одна тетрадь осталась). Учитель показывает, как записать примеры на деление с остатком: 3:2=1 (ост. 1); 4:2=2, 5:2=2 (ост. 1). Необходимо показать, как сделать подбор частного. Например, надо 7:3, а 7 на 3 не делится. Делим на 3 число, на 1 меньшее 7, т. е. отнимаем 1 от 7 единиц, получаем 6; 6:3=2, остаток 1. Учитель знакомит учащихся и с проверкой деления с остатком 5:2=2 (ост. 1).

Проверка. 2x2+1=4+1=5.

Обязательно нужно не только говорить, что остаток должен быть меньше делителя, но и каждый раз спрашивать, какой оста­ток получился, и сравнивать его с делителем.

При решении примеров на деление с остатком учитель подби­рает примеры для решения в такой последовательности: сначала остаток должен быть равен 1, затем 2, 3, а потом уже любому числу:

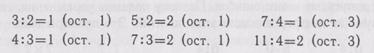
Предлагаются упражнения: в ряду чисел 5, 6, 7, 8, 9, 10, 11, 12 подчеркнуть те, которые делятся на 3 без остатка. Под числа­ми, которые не делятся на 3 (или любое другое данное число), записать остаток.

Цель таких упражнений заключается в том, чтобы учащиеся видели остаток, сравнивали его с делителем и убеждались в том, что остаток меньше делителя.

Изучение действий в пределах 100 заканчивается знакомством с правилом порядка действий. Учащиеся узнают, что если в при­мере есть действия сложение, вычитание, умножение и деление, то сначала выполняются умножение и деление (это действия пер­вой ступени), а потом по порядку сложение и вычитание (это действия второй ступени).

Пример:

ВНЕТАБЛИЧНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ

После изучения табличного умножения и деления учащиеся знакомятся с умножением круглых десятков и двузначных чисел на однозначное число, а также с умножением однозначных чисел на круглые десятки и двузначные числа, когда произведение не превышает 100 (20x3, 15-3, 4x20, 5-13), и соответствующими им случаями деления (60:3, 39:3, 80:20, 65:13). Все эти случаи умножения и деления относятся к внетабличному умножению и делению. Различные случаи внетабличного умножения и деления неодинаковы по сложности и поэтому изучаются в 5—6-х классах школы VIII вида. Так, умножение и деление круглых десятков на однозначное число (30x2, 60:2) и двузначного числа на одно­значное без перехода через разряд (12x3, 36:3) изучаются в 4-м классе. Случаи умножения и деления двузначного числа на одно­значное с переходом через разряд (15-2, 30:2, 18x3, 54:3) и деления на круглые десятки (40:20) изучаются в 6-м классе. Случаи умножения и деления на двузначное число (3-25, 75:25) изучаются в 7-м классе:

а) умножение и деление круглых десятков на однозначное
число (20x3).

Умножение круглых десятков на однозначное число сводится к табличному умножению. Например: 20 — это 2 десятка. 2 дес.хЗ=6 дес.=60. Пример можно проиллюстрировать с помо­щью брусков арифметического ящика и счетов.

Деление круглых десятков также сводится к табличным случа­ям деления: 60:3=? 60 — это 6 десятков. 6 дес.:3 = 2 дес.=20;

б) умножение и деление двузначных чисел на однозначное без
перехода через разряд.

В случаях 12x3 и 36:3 используется прием разложения перво­го множителя и делимого на разрядные слагаемые, последователь­ного умножения или деления каждого слагаемого и сложение результатов:

5. Составьте 10—12 упражнений на закрепление табличного умножения
(деления).

6. Выпишите из учебника математики для 4-го класса 8—10 упражнений
на закрепление таблицы умножения (деления), направленных на развитие
памяти учащихся.

в) умножение и деление на круглые десятки.

Умножение однозначного числа на круглые десятки объясняет­ся на основе переместительного закона умножения: 3-20=20-3. 20x3=60, значит, 3-20=60. Решение 60:20 рассматривается как деление по содержанию: 6 дес.:2 дес.=3. (Сколько раз 2 десятка содержится в 6 десятках?)

Со случаями внетабличного умножения и деления с переходом через разряд учащихся знакомят приемами письменных вычисле­ний:

Вопросы и задания

1. Какова последовательность изучения табличного умножения и деления в школе VIII вида?

^2. На основе анализа программы установите, в каких классах специаль­ной школы VIII вида и в каком объеме изучаются табличное умножение и деление.

3. Составьте фрагменты уроков на темы: 1) «Умножение — это сложение
равных слагаемых», 2) «Деление на равные части», 3) «Таблица умножения
числа 2», 4) «Таблица деления на 3», 5) «Переместительное свойство умно­
жения».

4. Составьте фрагменты уроков на темы: «Умножение», «Деление».
182

Глава 12

МЕТОДИКА ИЗУЧЕНИЯ ПЕРВОЙ ТЫСЯЧИ

ОБУЧЕНИЕ НУМЕРАЦИИ В ПРЕДЕЛАХ 1000

При обучении нумерации в пределах 1000 учащиеся знакомят­ся с сотней — новой счетной единицей, учатся считать сотнями, как раньше считали единицами и десятками, узнают десятичный состав чисел в пределах тысячи.

Изучение нумерации в пределах 1000 вызывает не меньше трудностей, чем изучение нумерации в пределах 100. Многие учащиеся не могут представить себе реального значения 1000, т. е. количества реальных предметов, которые обозначаются чис­лами в пределах 1000. Как и при изучении сотни, затруднение вызывает счет с переходом к новой сотне, а также к новому десятку, например: «... двести девяносто девять, двести девяносто десять, двести девяносто одиннадцать» или «...двести девяносто девять, двести девяносто сто», «...пятьсот двадцать девять, шесть­сот» и т. д. Счет в обратном порядке усваивается медленнее, чем в прямом. Больше затруднений, чем при изучении сотни, вызыва­ет решение задачи назвать число на единицу больше данного (когда есть переход к новой сотне), например 599. Вместо 600 учащиеся могут ответить: «Пятьсот девяносто десять». Особенно трудно учащимся назвать число на единицу меньше данного.

По-прежнему многих учащихся затрудняет понимание позици­онного значения цифр в числе. Особенно много ошибок встречает­ся при записи чисел с отсутствующими единицами того или иного разряда: вместо 805 они пишут 85, вместо 850 пишут 85. Затруд­няет и чтение таких чисел. Отдельные учащиеся записывают число начиная не с высшего разряда, а с разряда единиц, ставя его на первое место слева.

Большие затруднения испытывают учащиеся при усвоении де­сятичной системы счисления, т. е. при усвоении основы системы (10 единиц одного разряда образуют единицу следующего разря­да — 10 сотен образуют 1 тысячу).

Приступая к изучению нумерации в пределах 1000, учитель должен тщательно продумать систему изучения нумерации, подо­брать необходимые пособия, предусмотреть практические работы для учащихся, систему упражнений по закреплению нумерации при изучении последующих тем, коррекционно-развивающие уп­ражнения.

Последовательность изучения нумерации:

1. Получение круглых сотен. Запись круглых сотен. Счет круг­
лыми сотнями в прямом и обратном порядке.

2. Получение полных трехзначных чисел из сотен, десятков,
единиц. Запись полных трехзначных чисел.

3. Получение трехзначных чисел из сотен и десятков, из сотен
и единиц. Запись трехзначных чисел с нулем на конце или в
середине.

4. Счет единицами от 1 до 1000. Запись чисел от 1 до 1000.
Счет разрядными единицами по 1, 10, 100 и равными числовыми
группами (по 2, 5, 20, 50, 200, «250, 500).

5. Закрепление последовательности натурального ряда чисел
1 — 1000.

6. Закрепление нумерации в процессе изучения действий.

Несмотря на то что изучаются числа в пределах 1000, необхо­димость в использовании наглядных пособий и даже предметных пособий не снимается.

Наиболее распространенными пособиями, используемыми в школе VIII вида при изучении данной темы, являются: 1000 пало­чек, связанных в десятки и сотни; 10 квадратиков, каждый из которых разделен на 100 клеток; абак; счеты; таблицы с записью круглых сотен; таблицы с записью круглых десятков; разрядная сетка; таблица метрической системы мер; мерная веревка длиной 10 м, или 1000 см. Деньги: 1 р., 10 р., 100 р., 500 р.

\

Нумерация круглых сотен (устная и письменная)

Знакомство с устной нумерацией в пределах 1000 начинается с повторения: 1) счета единицами до 10; 2) замены 10 единиц одним десятком; 3) счета десятками до 100; 4) замены 10 десятков одной сотней. Например, учитель предлагает отсчитать 10 кубиков и спрашивает, сколько это десятков. Затем говорит: «Заменим 10 кубиков одним десятком (бруском). Сосчитаем десятками до 100, отсчитывая бруски или пучки палочек, 10 десятков чем можно заменить? 10 десятков — это 1 сотня (берем из арифметического

ящика пластину, которая разделена на 100 клеточек). Теперь счи­тать будем сотнями: 1 сотня — сто, 2 сотни — двести, 3 сотни — триста,..., 9 сотен — девятьсот, 10 сотен — тысяча». Учитель обращает внимание на то, что сотнями считают так же, как простыми единицами, и так же, как десятками.

По аналогии с обозначением 100 дается обозначение круглых сотен: в числе 100 одна сотня, сотни пишутся в числе на третьем месте справа, на месте единиц и десятков записываются нули; в числе двести 2 сотни, их пишут на третьем месте, а на месте единиц и десятков пишут нули. Так записываются цифрами все круглые сотни. Учитель вывешивает таблицу с записью единиц, круглых десятков и сотен. Дети читают числа, сравнивают, каки­ми единицами счета ведется счет в первом, во втором и третьем рядах. Сравниваются рядом стоящие числа в рядах и столбцах:

Счет до 1000 сотнями проводится и на других пособиях: на палочках, на абаке, на счетах. Пучок палочек из 10 сотен, 100 десятков, 1000 единиц наглядно представляет множество, состоя­щее из 1000 конкретных элементов.

Для некоторых учащихся полезно выполнить такое упражне­ние: на полу в классе или на большом листе бумаги начертить мелом квадрат, разделить его на 100 клеток (10 рядов, по 10 клеток в каждом) и предложить в каждую клетку положить по 10 зерен. Сколько зерен в каждом ряду? Сколько зерен в квадрате?

Ученики еще раз наблюдают образец множества, состоящего из 1000 элементов. Очень полезно сделать пособие «Тысяча». Каж­дый ученик чертит 10 квадратов и делить каждый на 100 клеток. Квадраты переплетаются, получается книжечка «Тысяча». На об­ложке книжечки ученики записывают: 1000 — это 10 сотен; 1000 — это 100 десятков; 1000 — это 1000 единиц.

Страницы книжечки заполняются числами. Первая страница — числами 1 —100, вторая страница 101—200 и т. д.

При работе со счетами некоторым ученикам, тем, которые долго не запоминают названия круглых сотен, на косточках тре­тьей проволоки можно написать: сто, двести, триста и т. д.

Счет сотнями связывается с раздроблением рублей и метров соответственно в копейки и сантиметры. Рассуждение проводится так: «1 р. — 100 к., значит, в 2 р. содержится 200 к., в 5 р. — 500 к. и т. д.».

Получение полных трехзначных чисел из сотен, десятков, единиц. Их запись

Учитель просит взять 1 сотню палочек, 2 десятка палочек и прибавить еще 3 палочки — получилось число сто двадцать три. Это число учащиеся должны отложить на счетах, на абаке, на пособиях из арифметического ящика.

Так учащиеся учатся составлять на разных пособиях числа из сотен, десятков, единиц, называть эти числа, а также называть числа, отложенные на счетах, на абаке и т. д.

Учащиеся лучше запоминают состав числа, чтение чисел, если работу по составлению, чтению и анализу чисел на пособиях связать с обозначением этих чисел цифрами.

При знакомстве с письменной нумерацией нужно учитывать, что большие затруднения у учащихся школы VIII вида вызывает запись чисел, в которых единицы одного или двух разрядов равны нулю. Поэтому здесь важно соблюдать определенную последова­тельность. Сначала следует познакомить учащихся с записью пол­ных трехзначных чисел, в которых все три разряда налицо, затем с записью чисел, в которых единицы первого или второго разряда равны нулю.

Запись чисел лучше всего дать сначала на абаке и выполнить анализ чисел. Например, чтобы отложить на абаке число 213, надо установить, что в этом числе сотен 2. Поставим цифру 2 в разряд сотен. Под десятками поставим цифру десятков — 1/. В разряд единиц поставим цифру 3. Мы записали число 213 цифра­ми. Сколько цифр в этом числе? Как называется число, которое записывается тремя знаками?

Наряду с обозначением чисел цифрами на абаке и чтением их необходимо использовать для обозначения чисел на письме табли­цы с круглыми сотнями круглыми десятками и едини­цами . Например, если на счетах отложено число 345, то учащиеся берут таблички и накладывают на круглые сотни круглые десятки, заполняя разряд десятков, а затем разряд единии . Может быть дано задание: «Взять круглые сотни, круглые десятки и единицы, из них составить число, прочитать

его, записать в тетрадь». Ученик выбирает таблички [7Ш|80У>] и составляет число 786.

Получение трехзначных чисел из сотен и десятков, сотен и единиц, их запись

Учитель берет одну сотню палочек. «Сколько это палочек?» — спрашивает учитель. Прибавили три десятка палочек или трид­цать: «Какое число получили из 1 сотни и 3 десятков?» «Сто тридцать», — отвечают ученики.

Так же составляются числа из сотен единиц. Например: «5 сотен и 7 единиц. Какое это число?» (Пятьсот семь.) Далее эти числа записываются в абак или в разрядную сетку. Учащиеся видят, что при записи этих чисел в конце числа или в середине пишется нуль. Ученики или учитель объясняет, почему в числе пишется нуль.

Затем дается задание составить число из круглых сотен и десятков , из круглых сотен и единиц

Можно дать и обратное задание: разложить числа 935, 730, 805 на разрядные числа. Учащиеся раскладывают в строчку

Полезно задание: назвать и записать число, которое состоит из 5 сот. 6 дес. 3 ед., 5 сот. 3 ед., 5 сот. 6 дес.

Затем проводятся упражнения на чтение чисел в разрядной сетке. Учащиеся чертят разрядные сетки в тетрадях и записывают в них числа. В разрядной сетке появляется четвертый разряд — единицы тысяч.

Когда учащиеся научатся составлять числа из сотен, десятков, единиц на различных пособиях, называть их, обозначать на пись­ме, анализировать по десятичному составу, необходимо перехо­дить к работе над закреплением последовательности натурального ряда чисел. Надо показать учащимся, что и все последующие числа после 100 также образуются путем прибавления к предыду­щему числу еще одной единицы или вычитанием из последующего числа единицы. Работа с наглядными пособиями в этот период также необходима, как и ранее.

Учитель предлагает взять одну сотню палочек (кубиков) и при­считать к ней еще одну палочку, получили сто один, прибавим еще одну палочку, получим сто два и т. д. Счет доводится до 199, затем прибавляется еще одна палочка. Образовалась новая сотня. 100 да еще 100 — двести. Проводится счет в прямом и обратном порядке в пределах 200. Затем счет продолжается от 200 до 300, от 300 до 400 и т. д. Особое внимание обращается на переход к новой сотне, новому десятку: 299, 300; 439, 440, что всегда за­трудняет учащихся. На последующих уроках вести счет от 1 до 1000 по единице нецелесообразно, так как занимает очень много времени. Поэтому счет проводится от заданного до заданного числа, куда включается счет на переход к новому десятку и сотне. Например: «Посчитай от 195 до 208, от 347 до 353, от 705 до 690, от 309 до 322, от 311 до 300» и т. д. Счет ведется единицами, десятками, сотнями и равными числовыми группами по 200, 250, 50, 20, 25, 5 в прямом и обратном порядке.

Необходимо, чтобы каждый ученик записал по порядку числа от 1 до 1000. Это задание учащиеся выполняют не сразу. Они записывают сначала числа первой сотни, затем второй и т. д. в клетки тех квадратов, которые заготовили раньше при изучении устной нумерации (в книжечку «Тысяча»). Эта работа может вы­полняться во внеурочное время как домашнее задание.

Отрабатывая запись и счет по таблицам каждой круглой сотни (от 100 до 200, от 200 до 300 и т. д.), учащиеся выделяют четные и нечетные числа, числа, оканчивающиеся нулем. Внутри каждой сотни ведется счет в прямом и обратном порядке как единицами, десятками, так и равными числовыми группами. Начинать счет можно единицами (101, 102,..., ПО), затем продолжить его десят­ками (110, 120,..., 200). Счет от 1 до 1000 проводится также разрядными единицами (1, 10, 100) или равными числовыми груп­пами. Например: «Считай сотнями: 100, 200, 300, 400,...»; «Счи­тай, прибавляя по 50 (равными числовыми группами): 450, 500, 550, 600»; «Считай, присчитывая по единице: 601, 602,..., 620»; «Считай, прибавляя по 5 (25): 625, 630, 635, 640, 645, 650, 675, 700» и т. д.

Учитель может предложить учащимся считать на пособиях: палочках, брусках и кубиках арифметического ящика, счетах. При счете кошф1Лных предметов учащиеся реальнее представляют себе переход к новому десятку, к новой сотне. Например, надо набрать из палочек число 309. Ученик должен взять 3 сотни

палочек и еще 9 палочек, присчитать еще одну единицу, заменить 10 палочек десятком палочек (т.е. связать в пучок) и считать дальше, прибавляя по одной палочке до 320.

Так же проводится счет в обратном порядке. Ученик берет 6 сотен палочек и ведет отсчет по 1: он берет (занимает) сотню палочек, развязывает этот пучок и получает 5 сотен и 10 десятков палочек. Затем развязывает десяток палочек и отнимает 1 палоч­ку. Остается 5 сотен 9 десятков и 9 единиц, т. е. 599.

Аналогичная работа проводится и на счетах. Это позволяет отработать переход к новому десятку, к новой сотне, размен де­сятков и сотен. Важно, чтобы учащиеся и на примерах могли показать образование последующего или предыдущего числа в числовом ряду путем прибавления или вычитания единицы:

Большое внимание при закреплении нумерации необходимо уделить анализу чисел, их сравнению.

Трехзначное число учащиеся учатся записывать по-разному: 234 — 2 сот. 3 дес. 4 ед., 234=200+30+4. Такая запись способствует усвоению десятичного состава чисел. Полезны и обратные задания: за­писать число, которое состоит из 7 сот. 3 дес. (7 сот. 3 дес. = 730), 700+5=705 и т. д.

Необходимо проводить упражнения на сравнение чисел: на­звать число на единицу больше (меньше) данного, увеличить (уменьшить) число на 1 единицу, на 1 десяток или на 1 сотню и записать его. Надо научить учащихся сравнивать числа, которые отличаются лишь цифрами, обозначающими число единиц, десят­ков или сотен, используя разностное, а где возможно, и краткое сравнение. Например:

— Сравните два числа: 124 и 128. Чем они отличаются? В чем их сходство? На сколько одно число больше другого?

- Сравните 124 и 24; 124 и 134; 275 и 375; 4 и 40; 4 и 400; 40 и 400; 2, 20, 200; 1, 10, 100, 1000.

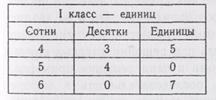
Процесс сравнения чисел облегчается, если их вписывать в разрядную сетку:

Необходимо учить детей сравнению чисел с высших разрядов. Если в одном числе сотен больше, чем в другом, то это число больше (на низшие разряды уже можно не смотреть); при равен­стве сотен надо сравнить десятки: то число будет больше, в котором число десятков больше, и т. д.

При сравнении чисел очень важно научить детей сравнивать разрядные единицы 1, 10, 100, 1000 и разрядные числа с одинако­вым числом единиц высших разрядов, например: 4, 40, 400.

Для сравнения эти числа записывают в разрядную сетку и выясняют, что каждое последующее число больше предыдущего в 10 раз и записано на месте следующего разряда:

Если 4 увеличить в 10 раз, то получится 40 (4x10= =40=4 дес.). Чтобы записать 40 в разрядную сетку, нужно цифру 4 поставить на второе место.

Если 40 увеличить в 10 раз, то получится 4 дес. х 10= =40 дес.=4 сотни. Цифру 4 надо записать на третьем месте в разрядной сетке.

Эти упражнения, если они выполняются систематически, по­зволяют учащимся сделать вывод о свойстве десятичной системы счисления: каждый последующий разряд больше предыдущего в 10 раз, и наоборот.

Весьма важным при изучении нумерации является различение учащимися количества разрядных единиц в числе и общего коли­чества единиц. Учащиеся должны понимать, что на первом месте справа стоят единицы, на втором — десятки, на третьем — сотни и т. д., и уметь отвечать на такие вопросы: «Покажи и назови, сколько единиц в числе, сколько десятков в числе. Покажи, где стоят в числе 348 десятки, единицы. Назови, сколько их».

Важно, чтобы дети научились определять, сколько всего еди­ниц (десятков, сотен) в числе. Отработать это понятие гораздо труднее, тем более что учащиеся слабо дифференцируют сходные

по звучанию вопросы: «Сколько единиц в числе? Сколько всего единиц в числе?» Опыт показывает, что целесообразнее вначале показать учащимся определение общего количества десятков в числе. Например: «Сколько десятков в числе 20? Сколько десят­ков содержится в числе 200? Как это узнать? (В одной сотне 10 десятков. В двух сотнях 10 дес. х2=20 дес.) Сколько десятков в числе 220? (200 — это 20 дес.; 20 — это 2 дес.; 220 — это 22 дес.; 348 — это 30 дес. да 4 дес. — всего 34 десятка.) Чтобы узнать, сколько всего десятков в числе, надо закрыть единицы и прочитать оставшееся число».

Затем проводятся упражнения на дифференциацию вопросов: «Сколько всего десятков в числе? Сколько десятков в числе?»

На этом этапе изучения нумерации целесообразно познакомить учащихся с классом единиц. Учитель рассказывает, что единицы, десятки и сотни объединяются (составляют) в класс единиц — это первый класс. Позже, когда они будут знакомиться с числами до 1 миллиона, они узнают о других разрядах и классах.

Разрядную таблицу учитель дополняет до таблицы классов и разрядов, которую учащиеся чертят в тетрадях и вписывают в нее трехзначные числа. Анализируют числа по десятичному составу, называя не только разряды, но и класс. Такого характера упраж­нения являются пропедевтикой понимания сущности десятичной системы счисления. Полезно при записи трехзначных чисел под диктовку без таблицы предварительно ставить три точки и запи­сывать каждую цифру разряда над соответствующей этому разря­ду точкой. Например, учитель просит записать число 325, спраши­вает, сколько цифр в этом числе. Просит школьников по­ставить три точки и над точка­ми записать число 325. Особен­но такой прием помогает уча­щимся при записи числа с нуля­ми в середине или в конце (507, 460), как известно, умственно отсталые школьники при записи таких чисел пропускают нули, вписывают лишние или переставля­ют. Например, вместо 507 записывают: 5007, 570.

Чтобы определить, сколько всего единиц в числе, рассуждения проводятся так: «В числе 486 4 сотни содержат 400 единиц, 8 десятков содержат 80 единиц и еще 6 единиц. Всего в числе 486 единиц».

С темой «Нумерация» тесно связано изучение метрической сис­темы мер длины и массы. Знакомство с килограммом и километ­ром, раздробление их соответственно в граммы и метры, счет по 100 г, по сотне метров, изучение соотношения мер позволяют еще раз закрепить счет разрядными единицами в пределах 1000 и соотношение между ними.

Работая с опережением, учитель, закрепляя работу над нумера­цией в 5-м классе, может познакомить учащихся с объединением известных им трех разрядов (единиц, десятков, сотен) в класс единиц и начинать анализ трехзначного числа с выделения клас­са, а потом разрядов, например: 475 — трехзначное число, состо­ит из класса единиц, 3 разрядов (единицы, десятки, сотни).

С темой «Нумерация» тесно связано решение примеров на все четыре арифметических действия с круглыми сотнями вида 300+100=400, 500-200=300, 200x2=400, 400:4=100.

На знании свойств натурального ряда чисел основано реше­ние примеров вида 432 + 1=433, 538-1=537, 599+1=600, 400-1=399.

Не нашли, что искали? Воспользуйтесь поиском: