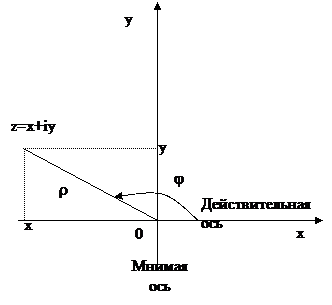ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Геометрическое представление комплексных чисел.
Для геометрического представления к.ч. используют точки и векторы координатной плоскости. В качестве к.ч. 
используют точку с абсциссой а и ординатой b.
|
Если к.ч. 
0, то его можно представить в виде
тригонометрическая форма к.ч,
где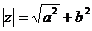 
модуль к.ч
Угол 
- угол, образованный 
с осью OX, назначенный аргументом к.ч. и обознается 
, причем tg 
Чтобы перейти от алгебраической формулы к.ч к тригонометрической и обратно, необходимо сделать следующие преобразования:
, 
, 
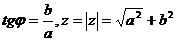Пример.
. Составить тригонометрическую форму к.ч. и изобразить его?
Действия над к.ч. в тригонометрической форме:
Практическое занятие 7.
Действия над комплексными числами.
Задача 1. 
найти: 
Задача 2. Построить к.ч. A(-1), B(i), C(-2), D(-3i), E(2-3i),F(-4-2i), M(3+i),
N(-6+2i), P(2+2i), K(-2+2i), L(-2-2i).
Задача 3. Представить в тригонометрической форме к.ч.
Задача 4. представить в тригонометрической форме к.ч.
Не нашли, что искали? Воспользуйтесь поиском: