
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Частные производные
Дана функция двух переменных Z=F(x,y),дадим аргументу x приращение Bx, а арг. Y менять не будем, Т.Е. перейдем от точки с координатами (x,y) к точке с координатоми (x+bx,y).
Тогда функция F(x,y) получит приращение  ,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
Опр.10.1: 


Он над частной производной ф-ии
F(x,y) и обозн. 
Аналогична опред-ся ч.пр. F(x,y) по Y


Т.Е ч.пр.  это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр
это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр  это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
Пр; Найти ч.пр. ф-ии 


Задачи:
1.  6.
6. 
2.  7.
7. 
3. 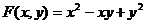 8.
8. 
4. 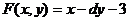 9.
9. 
5. 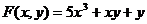 10.
10. 
Глава 2. Ряды.
Числовые ряды.
Ряды бывают: числовые, функциональные, степенные, конечные и бесконечные, знакопеременные.
Опр.1.1. Числовым рядом называется выражение вида  , где
, где 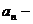 числа.
числа.
Для сокращенного обозначения рядов используют знак 
Пример. 
Опр. 1.2. Сумма первых n элементов ряда называется частичной суммой ряда  .
.

Опр. 1.3. Ряд называется сходящимся, если последовательность его частичных сумм сходится, т.е.  , где S – сумма ряда. (если предел не существует или равен
, где S – сумма ряда. (если предел не существует или равен  , то ряд расходится).
, то ряд расходится).
Пример. Определить сходимость ряда  - геометрическая прогрессия.
- геометрическая прогрессия.

Докажем сходимость каждого ряда.
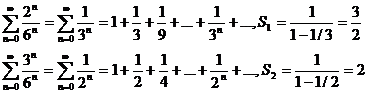
Эти ряды являются рядами бесконечной геометрической прогрессии со знаменателем <1, тогда  . Так как сумма ряда конечное число, то ряд сходится.
. Так как сумма ряда конечное число, то ряд сходится.
Т. 1.1. (Необходимый признак сходимости рядов).
Если ряд сходится, то его общий элемент стремится к нулю, т.е.  .
.
Пример.  ряд расходится.
ряд расходится.
Признак Даламбера сходимости рядов.
Пусть дан ряд  Допустим, что
Допустим, что  , тогда
, тогда
1) Если p<1, то ряд сходится.
2) Если p>1, то ряд расходится.
Пример.  ряд сходится.
ряд сходится.
Задача. Написать первые пять элементов ряда по заданному общему элементу и проверить сходится ли ряд.

Не нашли, что искали? Воспользуйтесь поиском: