Множества и отношения.

Опр. 1.1. Множество это совокупность объектов, которые объединены как-либо свойствами.

1. Z - Множество целых чисел

2. Q - Множество рациональных чисел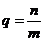

3. N - Натуральные числа (1,2,3…)

4. R - Действительные числа

5. C - Комплексные числа

Опр.1.2. Подмножеством В данного множества А называется множество, которое содержит некоторые элементы мн. А или множество, каждый элемент которого принадлежит мн.А.

Обозн.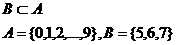

Пустое множество это множество, которое не содержит ни одного элемента.

Обозн. Ø

Опр.1.3. пересечением двух множеств А и В называется множество, каждый элемент которого принадлежит одновременно и множеству А, и множеству В.

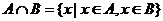
Опр. 1.4. Объединением двух множеств А и В называется множество, каждый элемент которого принадлежит или множеству А, или множеству В, или одновременно двум множествам.

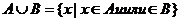
Опр.1.5. Разностью множеств А и В называется множество только тех элементов множества А, которые не принадлежат В.

Опр.1.6. . Дополнением множества В до множества А называется множество таких элементов, которые принадлежат А, и не принадлежат В.

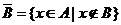
Пример. А={0,1,2,…,9}, В={5,6,7,…,15}, C={0,1,2,…,15}

Найти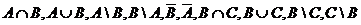

Операции над множествами можно проиллюстрировать с помощью диаграмм Эйлера.

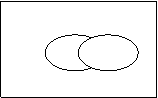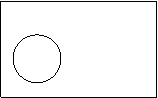Опр. 1.7. Два множества А и В называются равными, если каждый элемент множества А принадлежит В и наоборот.

Задача 1. С помощью диаграмм Эйлера найти

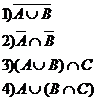
Задача 2. А={0,1,2,3,4,5,6}, B={1,2,3,4,6,8}, C={-1,0,3,4,7,8}

Найти

Самостоятельно

А={0,1,2,3}, B={-1,2,3,4,5,6}

Найти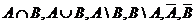

Не нашли, что искали? Воспользуйтесь поиском: