
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Математическое ожидание и дисперсия случайной величины.
Числовыми характеристиками сл.в. являются математическое ожидание M(X), дисперсия D(X), среднее квадратичное отклонение 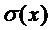 .
.
Опр.3.1. Математическим ожиданием дискретной сл.в. Х с законом распределения называется число
| Х | х1 | х2 | х3 | … | хn |
| Р | р1 | р2 | р3 | … | рn |
M(X)=x1p1+x2p2+…+xnpn
Пример. Найти М(Х) числа очков, выпадающих при бросании игральной кости.
Решение. Закон распределения имеет вид
| Х | ||||||
| Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Тогда М(Х)= 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6=3,5
Свойства М(Х):
1. М(СХ)=С*М(Х).
2. М(Х+У)=М(Х)+М(У)
3. М(Х*У)=М(Х)*М(У)
Опр.3.2. Пусть Х – дискретная сл.в., возможные значения которой х1,х2,…,хn,
М(Х) – математическое ожидание, тогда сл.в. Х-М(Х) называется отклонением величины Х от ее математического ожидания, т.е. отклонение это сл.в., которая принимает значения: х1-М(Х), х2-М(Х),…, хn-М(Х).
Опр.3.3. Дисперсией сл.в. называется математическое ожидание квадрата
отклонения сл.в. от ее математического ожидания.
Дисперсия обозначается 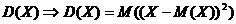
Опр.3.4. Средним квадратичным отклонением сл.в. Х называется корень
квадратный из дисперсии.  .
.
На практике часто используют формулу  .
.
Пример. Дискретная сл.в. имеет закон распределения
| Х | |||
| Р | 0,3 | 0,5 | 0,2 |
Найти D(X)? 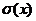 ?
?
Решение: М(Х)= 0*0,3+1*0,5+2*0,2=0,9
Запишем закон распределения отклонения этой величины, т.е. величины 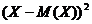
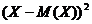
| (0-0,9) 
| (1-0,9) 
| (2-0,9) 
|
| Р | 0,3 | 0,5 | 0,2 |
D(X)=(0-0,9)  *0,3+(1-0,9)
*0,3+(1-0,9)  *0,5+(2-0,9)
*0,5+(2-0,9)  *0,2=0,81*0,3+0,01*0,5+1,21*0,2=0,49.
*0,2=0,81*0,3+0,01*0,5+1,21*0,2=0,49.
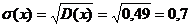
Задача. Найти М(Х)? D(X)? 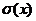 ? Сл.в., заданной по закону:
? Сл.в., заданной по закону:
| Х | ||||
| Р | 0,3 | 0,1 | 0,2 | 0,4 |
Не нашли, что искали? Воспользуйтесь поиском: