Дифракция от прямолинейного края полуплоскости

Будем рассматривать плоскую волну. Пусть полуплоскость (ПП) совпадает с одной из волновых поверхностей. Разобьем ее на зоны, параллельные краю ПП. Ширину зон выбираем так, чтобы расстояния от точки Р до краев зон отличались на одинаковую величину Δ (для удобства построения векторных диаграмм). Зоны с номерами m и m’ имеют

одинаковую ширину и расположены относительно точки Р симметрично, в результате создаваемые ими в точке Р колебания совпадают по амплитуде и фазе. Амплитуда колебаний пропорциональна площади зон, т.е. их ширине. Суммарная ширина первых m зон равна: d₁+d₂+…+d_m= , т.к. зоны узкие, Δ<<b, поэтому, если m не слишком велико, вторым членом под корнем пренебрегаем. Тогда d₁+d₂+…+d_m= . Если m=1, то d₁= , тогда d₁+d₂+…+d_m= d₁√m. Расчет по этой формуле дает, что d₁:d₂: d₃:…:d_m=1:0,41:0,32:0,27:…Также соотносятся и площади зон. Т.е. в отличие от сферической волны (и кольцевых зон) амплитуды колебаний, создаваемых с точке Р соседними зонами, сначала убывают быстро, а затем – медленнее. Поэтому величина амплитуды для кольцевых зон принята постоянной и будет иметь вид а), а для прямолинейных зон – убывающей –вид б) (для колебаний, вызванных зонами справа -1,2,3…). Если добавить колебания от зон, расположенных слева – 1’,2’,3’ –то получим спираль Корню.

а)	б)	Спираль Корню

Точки F₁ и F₂, к которым асимптотически приближается кривая, называются фокусами или полюсами спирали Корню. Уравнение спирали Корню в параметрической форме имеет вид: 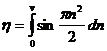интегралы Френеля. v –дина дуги спирали от начала координат.

Спираль Корню позволяет найти амплитуду светового колебания в любой точке экрана. Для точки, лежащей на границе геометрической тени (х=0) все зоны, расположенные слева (1’,2’,3’) будут закрыты. Если точка смещается влево, то все большее число нештрихованых зон закрывается. Поэтому начало результирующего вектора перемещается по правому витку к направлению полюса F₁. В результате амплитуда монотонно уменьшается до нуля. Если точка Р смещается вправо, в дополнении к нештрихованным, открывается все больше штрихованных зон. Поэтому начало результирующего вектора по левому витку к полюсу F₂.

Дифракция от щели

Рассмотрим подробнее дифракцию Френеля от бесконечно длинной

щели. Ее можно получить, расположив рядом две полуплоскости, тогда задачу о дифракции Френеля от щели можно решить с помощью спирали Корню. Для точки Р, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали. Если сместиться в точку Р’, лежащую против края щели, начало результирующего вектора переместиться в середину спирали О, а конец –переместиться по спирали в направлении полюса F₁. При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и, наконец, окажутся на минимальном расстоянии (Р’’), соответственно и интенсивность будет минимальна. При дальнейшем движении точки Р влево, начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. Если двигать точку Р вправо от середины, картина будет симметрична. Если изменять ширину щели, интенсивность в средней точке Р будет пульсировать, проходя через максимумы и отличные от нуля минимумы.

	максимумы	минимумы

Не нашли, что искали? Воспользуйтесь поиском: