Теоретические основы

Декартово произведение (прямой декартово произведение) множеств X и Y - это множество всех возможных упорядоченный пар или кортежей, первыми компонентами которых являются элементы множества X, а вторыми - элементы множества Y.

Декартово произведение множеств X и Y обозначается как X Y: X Y = {(x, y) | x ∈ X ∧ y ∈ Y}. Здесь упорядоченная пара (x, y) элементов x, y есть множество {{x}, {x, y}}, которая имеет такое свойство, что (x, y) ≠ (y, x).

Пусть задано множество и пусть и — элементы этого множества (при этом может случиться, что ). Назовем упорядоченной парой, а и — компонентами или координатами этой пары. Например, число 35 записывается с помощью двух цифр 3 и 5. Это следует делать в определенном порядке: сначала 3, а потом 5. Если их переставить, получится другое число — 53. Говорят, что — упорядоченная пара чисел. В число 44 входят две одинаковые цифры. Они образуют упорядоченную пару . Таким образом, в упорядоченных парах числа могут повторяться.

Пары и считаются совпадающими в том и только том случае, когда и . Поэтому, если , то пары и 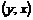различны.

Упорядоченные пары можно составлять не только из чисел, но и из элементов любых множеств.

Например, из букв множества можно составить девять упорядоченных пар: . Примером упорядоченной пары натуральных чисел может служить пара, составленная из числителя и знаменателя дроби — вместо того, чтобы писать , можно записать . При перестановке чисел 3 и 5 получается иная дробь .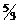

Еще более общее понятие упорядоченной пары получается, если брать ее компоненты из различных множеств. Например, компоненту из множества , а — из множества . Пусть, например, заданы два множества и . Образуем из элементов этих множеств пары так, чтобы первая компонента пары принадлежала множеству , а вторая множеству . Все эти пары составляют множество: , которое является декартовым произведением множеств и , обозначают .

Определение. Декартовым произведением множеств и называют множество , элементами которого являются все пары такие, что , , т. е. .

Если множества и совпадают, т. е. , то множество состоит из всех пар таких, что , .

Полагают, что для любого множества .

Элементами множества являются пары такие, что и , а элементами множества 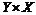— пары , где
и . Но при пары и 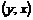различны. Следовательно, если , то множества и 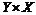различны.

Элементы декартова произведения двух конечных множеств удобно располагать в виде таблицы, где по вертикали располагают элементы множества , по горизонтали — элементы множества , а элементы множества пишут на пересечениях соответствующих строк и столбцов.

Например, на таблице, приведенной ниже, изображены элементы декартова произведения множеств и .

	(а; 4)	(а; 5)
	(в; 4)	(в; 5)
	(с; 4)	(с; 5)

Если задано множество , то из его элементов можно составлять
не только упорядоченные пары, но и упорядоченные тройки элементов, четверки элементов и т. д. Например, буквы слова «число» образуют упорядоченную пятерку. Введем общее математическое понятие, частными случаями которого являются и упорядоченные пары, и упорядоченные тройки, и упорядоченные четверки и т. д.

Пусть даны множества . Возьмем какой-нибудь элемент из множества , потом элемент из множества ,..., элемент — из множества . Выбранные элементы расположим по порядку: . Получаем упорядоченную -ку элементов (читается: «энка»), выбранных из множеств . Вместо слов «упорядоченная -ка» говорят короче — «кортеж» (французское слово «кортеж» означает торжественное шествие, например, говорят «свадебный кортеж» или «кортеж автомашин»). Число называют длиной кортежа, элементы — его компонентами.

Множества могут иметь общие элементы или даже совпадать друг с другом. Например, слово «математика» — кортеж длины 10, составленный из элементов множества (при этом в слово «математика» входят не все буквы этого множества, а лишь часть этих букв). Предложение «Математика — царица всех наук» — кортеж длины 4, компонентами которого являются слова русского языка. Каждое из этих слов — кортеж, составленный из букв. Таким образом, компонентами кортежа могут быть и кортежи. Можно составлять и кортежи, компонентами которых являются множества, например: .

В математике примером кортежа может служить набор цифр, входящих в десятичную запись какого-нибудь числа. Этот кортеж составлен из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, причем цифры могут повторяться, а при перестановке цифр может получиться иное число. Так, кортеж цифр числа 112231 имеет вид .

Определение. Два кортежа и называют равными, если они имеют одинаковую длину, т. е. , и каждая компонента первого кортежа равна компоненте второго кортежа с тем же номером, т. е. , например, кортежи
и равны, а кортежи и 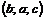не равны.

Используя понятие кортежа, можно определить понятие декартова произведения трех, четырех и, вообще, множеств. Пусть заданы множеств: (множества могут иметь общие элементы). Из элементов этих множеств образуем кортежи длины , первая компонента которых принадлежит множеству , вторая — множеству ,..., -я — множеству . Множество таких кортежей называют декартовым произведением множеств и обозначают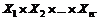

Не нашли, что искали? Воспользуйтесь поиском: