ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ

Множество В включается в множество А, если каждый элемент множества В является также элементом множества А. Множество В является подмножеством или частью множества А. Символическая запись: .

Отношение включения обозначается символом , т. е. предложение “множество В включается во множество А” записывается: В А.

Поскольку множество можно изобразить в виде геометрических фигур, логические рассуждения тоже изображаются геометрически.

Метод геометрической иллюстрации логических рассуждений был предложен великим математиком 18 века петербургским академиком Леонардом Эйлером (1707–1783) и широко применялся английским математиком Джоном Венном (1834–1923), т.е. для наглядности множества и логические рассуждения изображаются в виде кругов, которые называются кругами Эйлера или диаграммами Эйлера-Венна.

Например:

1) N Z Q R C.

2) Множество прямоугольников во множество параллелограммов множество четырёхугольников.

Частным случаем включения является равенство.

Два множества, состоящие из одних и тех же элементов называются равными (А = В).

Символическая запись: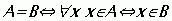

Как показывают приведённые выше примеры, если В А, то возможны два случая:

1) Существует хотя бы один элемент множества А, не принадлежащий множеству В. В таком случае говорят, что В — собственная часть (или собственное подмножество) А, или что В строго включается в А. Отношение строгого включения обозначается: В А.

2) Не существует ни одного элемента множества А, не принадлежащего В. Этот случай равносилен отношению 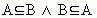, т. е. равенству А = В.

Не нашли, что искали? Воспользуйтесь поиском: