Практические задания. 1. Фирма имеет 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В

Вариант № 1

1. Фирма имеет 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В, С. Продукцию всех трех видов выпускают 10 предприятий, продукцию А и В – 18 предприятий, продукцию А и С – 15 предприятий, продукцию В и С – 21 предприятие. Число предприятий, выпускающих продукцию А равно числу предприятий, выпускающих продукцию В и равно числу предприятий, выпускающих продукцию С. Найти число всех предприятий.

2. Упростить: È È .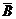

3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?

4. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А È В = С.

5. Эквивалентны ли множества A = { x: x ² – 8 x + 15= 0} и B = {2, 3}?

Вариант № 2

1. В группе спортсменов 30 человек. Из них 20 занимаются плаванием, 18 – легкой атлетикой и 10 – лыжами. Плаванием и легкой атлетикой занимаются 11 человек, плаванием и лыжами – 8, легкой атлетикой и лыжами – 6 человек. Сколько спортсменов занимаются всеми тремя видами спорта?

2. Упростить: A (A È B).

3. В каком случае А А  В?

4. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А È В = С.

5. Какое из множеств A = {1, 4, 9, 16, 25,…} и B = {1, 1/2, 1/4, 1/6, 1/8,…} имеет большую мощность?

Вариант № 3

1. В студенческой группе 20 человек. Из них 10 имеют оценку “отлично” по английскому языку, 8 - по математике, 7 - по физике, 4 - по английскому языку и по математике, 5 - по английскому языку и по физике, 4 - по математике и по физике, 3 - по английскому языку, по математике и по физике. Сколько студентов группе не имеют отличных оценок?

2. Упростить: (A \ B) È (A \ B).

3. Найти все подмножества множества A = {1, 2, 3, 4).

₄

4. Пусть A _n = {0, 1/2ⁿ}. Найти U A _n.

ⁿ⁼¹

5. Доказать, что множества точек контуров всех треугольников эквивалентны.

Вариант № 4

1. В классе 20 человек. На экзаменах по истории, математике и литературе 10 учеников не получили ни одной пятерки, 6 учеников получили 5 по истории, 5 – по математике и 4 – по литературе; 2 - по истории и математике, 2 - по истории и литературе, 1 - по математике и литературе. Сколько учеников получили 5 по всем предметам?

2. Упростить: (A  B) È (A  B).

3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?

4. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А È В = С.

5. Эквивалентны ли множества A = {2 ^x, 0< x < ¥} и B = {2ⁿ, n = 1, 2, …}?

Контрольные вопросы

1. Пусть a Î А. Следует ли отсюда, что { a } А?

2. В каком случае А А  В?

3. Назовите множество, которое является подмножеством любого множества.

4. Может ли быть множество эквивалентно своему подмножеству?

5. Мощность какого множества больше: множества натуральных чисел или множества точек отрезка [0, 1]?

Список литературы

Не нашли, что искали? Воспользуйтесь поиском: