Теоретические основы. Эйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов

Эйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783).

Таблица 1

Название операции	Обозначение	Изображение	Определение	Символическая запись	Лог. операции
Пересечение множеств			Те и только те элементы, которые принадлежат одновременно А и В		Λ
Объединение множеств			Те и только те элементы, которые принадлежат хотя бы одному из множеств А или В		V
Разность множеств			Те и только те элементы, которые не принадлежат В
Дополнение к множеству А			Те и только те элементы, которые не принадлежат А (т.е. дополняют его до универсального U)
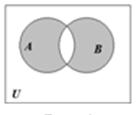
Симметрическая разность			Те и только те элементы, которые принадлежат одному из множеств: А либо В, но не являются общими элементами

Пример 1

Экзамен по математике содержал три задачи: по алгебре, по геометрии и по тригонометрии. Из 650 абитуриентов задачу по алгебре решили 400 абитуриентов, по геометрии – 480, по тригонометрии – 420. Задачи только по алгебре и геометрии решили 100 человек, только по геометрии и тригонометрии – 90 человек. Задачу только по тригонометрии решили 85 человек, только по геометрии – 75 человек.

Сколько абитуриентов решили только одну задачу?

Решение:

Введём обозначения:

А – множество абитуриентов, которые решили задачи по алгебре;

Г – множество абитуриентов, которые решили задачи по геометрии;

Т – множество абитуриентов, которые решили задачи по тригонометрии.

По условию, знаем мощности:

m(A∩Г)=100, m(Г∩Т)=90, m(Т)=85, m(Г)=75.

Нам надо найти количество абитуриентов, которые решили только одну задачу, т.е. m(A)+m(Т)+m(Г), где неизвестно только m(A) – количество абитуриентов, которые решили только алгебру.

Из условия, Геометрию решили 480 абитуриентов, следовательно:

m(А∩Т∩Г)=480-m(Г)-m(A∩Г)-m(Г∩Т)=480-75-100-90=215 – количество абитуриентов, которые решили все три задачи.

Из условия, Тригонометрию решили 420 абитуриентов, следовательно:

m(А∩Т)=420-m(Т)-m(A∩Т∩Г)-m(Г∩Т)=420-85-215-90=30 – количество абитуриентов, которые решили только Алгебру и Тригонометрию.

Из условия, Алгебру решили 400 абитуриентов, следовательно:

m(A)=400- m(A∩Г)- m(А∩Т∩Г)- m(А∩Т)=400-100-215-30=55 – количество абитуриентов, которые решили только Алгебру.

Итак, m(A)+m(Т)+m(Г)=55+85+75=215 – количество абитуриентов, которые решили только одну задачу.

Так как всего 650 абитуриентов, то должно выполняться равенство:

m(AUТUГ)=m(A)+m(Т)+m(Г)+m(A∩Г)+m(А∩Т)+m(T∩Г)+ m(А∩Т∩Г)=215+100+30+90+215=650 – верно.

Ответ: 215 абитуриентов решили только одну задачу.

Не нашли, что искали? Воспользуйтесь поиском: