Теоретические основы. Основные понятия множества

Основные понятия множества

Определение 1.1. Множеством называется совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты. Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое".

Пример 1.1.

Следующие совокупности объектов являются множествами: множество деревьев в лесу, множество целых чисел, множество корней уравнения e^xsinx = 0.5.

Всякое множество состоит из элементов. Множества обозначают большими буквами, например А. В, С, а элементы – маленькими буквами, например, а, b, c.

Множество и его элементы обозначаются следующим образом:

А = { a ₁, a ₂, a ₃} – множество, состоящее из трех элементов;

А = { a ₁, a ₂, …} – множество, состоящее из бесконечного числа элементов.

Множество может состоять из элементов, которые сами являются множествами. Нужно различать элемент a и множество, состоящее из единственного элемента a.

Пример 1.2.

Множество А = {1, 2} состоит из двух элементов 1, 2; но множество { А } состоит из одного элемента А.

Если элемент a принадлежит множеству А, это записывается следующим образом:

a Î А. Если элемент a не принадлежит множеству А, то записывают так: a Ï А.

Пример 1.3.

Пусть А ₁ – множество простых чисел, А ₂ – множество целых чисел, a = 4. Тогда

a Î А ₂, a Ï А ₁.

Если все элементы множества А являются элементами множества В и наоборот, т. е. множества А и В совпадают, то говорят, что А = В.

Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В, и записывают А Í В или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А Í А.

Если А Í В и В Í А, то по ранее введенному определению А = В.

Если А Í В и А ¹ В, то А есть собственное подмножество В, А Ì В. Если А не является собственным подмножеством В, то записывают А Ë В.

Пример 1.4.

Пусть А – множество четных чисел, В – множество целых чисел, С – множество нечетных чисел. Тогда

А Ì В, С Ì В, А Ë С, В Ë А.

Не надо смешивать отношение принадлежности (Î) и отношение включения (Í).

Пример 1.5.

Пусть А = {2} – множество, состоящее из одного элемента, В = {{2}, {4}} – множество, состоящее из двух элементов, каждое из которых является одноэлементным множеством. Тогда имеют место следующие соотношения:

2 Î {2};

{2} Ì {{2}, {4}};

2 Ï {{2}, {4}}.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ. Принято считать, что пустое множество является подмножеством любого множества, Æ Í А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.

Пример 1.6.

Множество корней уравнения sinx = 2 является пустым.

Множество всех подмножеств данного множества А называется множеством-степенью и обозначается P (A). Множество P (A) состоит из 2 ⁿ элементов (доказать самостоятельно).

Пример 1.7.

Пусть множество А = {1, 2} состоит из двух элементов 1, 2. Тогда множество P (A) включает в себя пустое множество Æ, два одноэлементных множества {1} и {2} и само множество А = {1, 2}, т. е.

P (A) = {Æ, {1}, {2}, {1, 2}}.

Мы видим, что множество P (A) состоит из четырех элементов (4 = 2²).

Существуют следующие способы задания множеств.

1. Перечислением элементов множества. Например:

A = {1, 3, 5, 7, 9} – конечное множество;

B = {1, 2, …, n, …} – бесконечное множество.

2. Указанием свойств элементов множества. Для этого способа пользуются следующим форматом записи: A = { a çуказание свойства элементов}. Здесь a является элементом множества A, a Î А. Например:

A = { a ç a – простое число} – множество простых чисел;

B = { b ç b ² – 1 = 0, b – действительное число} – множество, состоящее из двух элементов, B = {– 1, 1};

Z = { x ç 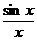= 1}– множество, состоящее из одного числа, x = 0.

Не нашли, что искали? Воспользуйтесь поиском: