Сильный и слабый экстремум в задачах классического вариационного исчисления.

Поставленные выше задачи обладают все еще неопределенностью, так как не описан класс допустимых элементов. Задача Лагранжа (6) – (9) с фиксированным временем в рамках классического вариационного исчисления будет исследоваться в банаховых пространствах , где 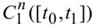– пространство непрерывно дифференцируемых вектор-функций, а – пространство непрерывных вектор-функций. Норму в пространстве C1 обозначим как , норму в пространстве C, если мы хотим сопоставить ее с нормой в пространстве C1, иногда будем обозначать . Исследование простейших задач проводится в банаховых пространствах Локальный минимум в пространстве в случае задачи Лагранжа, или в пространстве 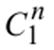в случае простейших задач, называется слабым. Иначе говоря, пара доставляет слабый локальный минимум функционалу в задаче (6) – (9), если найдется такое число e(эпсила) > 0, что для любой допустимой пары такой, что 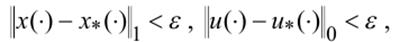, выполняется неравенство При этом пара называется допустимой в задаче, если она удовлетворяет

ограничениям (7) и (8) и граничным условиям (9). Совершенно аналогично определяется слабый минимум для простейшей векторной задачи (5).

Локальный экстремум по x в топологии пространства называется сильным. Иначе говоря, допустимая пара 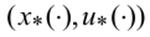дает сильный локальный минимум функционалу J в задаче (6) – (9), если найдется такое число e(эпсила)> 0, что для любой допустимой пары , для которой , выполняется неравенство 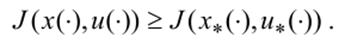Аналогичным образом определяется сильный минимум для простейшей векторной задачи (5).

Далее в термин «сильный экстремум» будет вкладываться несколько расширенное толкование, которое свойственно этому понятию в задачах оптимального управления. Об этом речь пойдет в следующем параграфе.

Не нашли, что искали? Воспользуйтесь поиском: