Задачи оптимального управления. Постановка задачи оптимального управления

В середине прошлого века в вариационном исчислении появился новый класс экстремальных задач – задачи оптимального управления. Одно из отличий этих задач от задач классического вариационного исчисления – наличие переменных, которые не обладают необходимой гладкостью и могут быть разрывными. Необходимое условие экстремума для задач этого класса имеет существенно иную форму в сравнении с классическими уравнениями Эйлера и Лагранжа. В качестве обязательного условия в решение задачи оптимального управления входит решение вспомогательной задачи на максимум. Отсюда и возникло название этого необходимого условия экстремума – принцип максимума.

Приведем формальную постановку задачи оптимального управления:

Найти среди всех допустимых управлений, переводящих фазовую точку из положения х₀ в положение x₁ , такое, для которого функционал

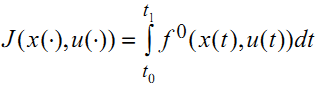
принимает наименьшее значение.

Функция f⁰ непрерывная по переменным x и u, непрерывно дифференцируемая по переменной x.

Управление u(·) , на котором достигается оптимальное значение данной задачи, называется оптимальным управлением, а соответствующая траектория x(t) – оптимальной траекторией. В этом смысле основная задача – найти оптимальные управления и соответствующие оптимальные траектории, другими словами, найти оптимальный управляемый процесс.

Для J = t₁ – t₀ оптимальность управления u(t) эквивалентна минимизации времени перехода из положения x₀ в положение x₁. Задача отыскания оптимальных управлений и траекторий в этом случае называется задачей об оптимальном быстродействии.

Не нашли, что искали? Воспользуйтесь поиском: