Доказательство принципа максимума для линейной задачи быстродействия.

Введем понятие сферы достижимости. Пусть 0 > T – верхняя граница на длины интервалов, на которых будут рассматриваться управления. Будем говорить, что точка x принадлежит сфере достижимости, если на интервале [t₀, t₁] существует допустимое управление u(t) и соответствующая ему траектория x(t) такие, что x(t₀) = , x(t₁) = 0, t₁ – t₀ ≤ T.

Лемма 1. Сфера достижимости V_Т является выпуклым множеством.

Доказательство. Пусть 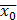, 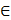V_T. По определению это означает, что существует допустимое управление , t [t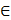₀, ], где ≤ t₀ + T, которое переводит фазовую точку x из положения 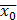в точку 0. Аналогично, существует допустимое управление , t [t₀, ], где ≤ t₀ + T, которое переводит фазовую точку x из положения в точку 0.

Можно считать, что = t₀ + T. В противном случае решим систему = f(x, u(t)) с начальным условием () = 0, доопределив управление (t) как показано на рисунке.

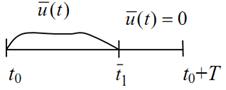
Получим, что (t) = 0 на интервале [ t₀ + T]. Аналогично, для (·) и (·) можно считать, что = t₀ + T. Пусть y₀ = λ + (1-λ) , 0≤λ≤1. Тогда управление u*(t)= λ (t) + (1-λ) (t), определенное на интервале [t₀, t₀ + T], является допустимым управлением. Ему соответствует траектория x*(t) = λ (t) + (1-λ) (t), по которой фазовая точка переходит из начального положения x*(t₀) = λ + (1-λ) = y₀ в конечное положение x*(t₀ + T) = 0.

Лемма 2. Если x₀ – внутренняя точка V_T, то из x₀ можно перейти в точку 0 за время строго меньше T.

Доказательство. Рассмотрим произвольную точку x₀ IntV_T. Из определения внутренней точки следует, что существует шар B(x₀, r) V_T. Так как из леммы 1 следует, что множество V_T выпукло, то по лемме Каратеодори существуют (n+1) точки z₁,…,z_n+1, расположенные внутри шара и такие, что симплекс, образованный ими, содержит x₀ строго внутри. Следовательно, в силу непрерывности расстояния найдутся достаточно малые окрестности точек z_j из V_T, такие, что симплекс, образованный этими точками из сферы достижимости, содержит x₀. Тогда по определению множества V_Т cуществуют допустимые управления u_s(t) на интервале [t₀, t₀ + T] такие, что x_s(t₀) = y_s, x_s(t₀ + T) = 0, s=1,…,n+1. Так как функции x_s(t) непрерывны, то существует ɛ > 0, для которого x₀ 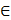IntCo{x₁(t₀ +ɛ),…,x_n+1(t₀ + ɛ)}. Но все точки x_s(t₀ + ɛ), s=1,…,n+1 лежат в сфере достижимости V_T-ɛ. Это означает, что x₀ 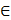V_T-ɛ.

Лемма 3. Пусть u(t) – допустимое управление на интервале [t₀,t₁], x(t) – соответствующее решение, P(t) – произвольное решение сопряженной системы = - PA на данном интервале. Тогда во всех точках непрерывности управления u(t) справедливы следующие равенства:

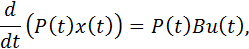
P(t₁)x(t₁) – P(t₀)x(t₀) = .

Доказательство. = (t)x(t) + P(t) (t) = -P(t)(Ax(t)+Bu(t)) = P(t)Bu(t). Перейдем к доказательству принципа максимума, то есть докажем, что оптимальное управление удовлетворяет P(τ)Bu*(τ) = , τ 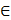[t_o,t₁].

Пусть u(t) – оптимально управление на интервале [t₀, t₁], x(t₀) = x₀, x(t₁) = 0. Положим, T = t₁ – t₀. Из леммы 2 следует, что x₀ – граничная точка сферы достижимости V_T. Следовательно, по теореме отделимости существует вектор d ≠ 0, такой, что для всех векторов х из множества V_T выполняется неравенство d(x-x₀) ≥ 0.

Пусть P – решение = - PA с начальным условием P(t₀) = . Для него выполняется равенство P(t)Bu(t) = для всех t из интервала [t₀, t₁]. Действительное, допустим противное: пусть существует 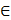[t_o,t₁] такое, что P()Bu()< . Это означает, что существует такое v 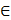U, что P()Bu()< P()Bv. Из непрерывности управления следует, что существует интервал [τ₀, τ₁] [t₀, t₁] такой, что P(τ)Bu(τ)<P(τ)Bv для всех τ 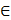[τ₀, τ₁]. Пусть

u*(t) =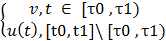

Очевидно, что u* - допустимое управление. Пусть x*(t) – соответствующая ему траектория и x*(t₁) = 0. Пусть x*₀ = x*(t₀). Имеем, что x*₀ V_T, и, следовательно, d(x*₀ – x₀) ≥0. Из леммы 3 имеем:

d(x*₀ – x₀) = P(t₀)(x*(t₀)-x(t₀))=(P(t₁)x(t₁)-P(t₀)x(t₀)) – (P(t₁)x*(t₁)-P(t₀)x*(t₀)) = = . Противоречие с неравенством, которое следует из теоремы отделимости.

Не нашли, что искали? Воспользуйтесь поиском: