Элементарный вывод необходимых условий экстремума для простейших задач классического вариационного исчисления

В этом параграфе дается вывод необходимых условий Эйлера. Дальнейшие рассуждения всюду основаны на непосредственном применении метода вариаций.

Начнем с простейшей задачи вариационного исчисления с закрепленными концами:

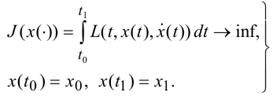(11)

Предположим, что функция L(t,x,y) непрерывно дифференцируема в некоторой области U пространства R³. Задачу (11) будем исследовать на слабый экстремум, то есть в пространстве C1([t0,t1]).

Вывод уравнения Эйлера состоит из трех этапов.

Первый этап состоит в доказательстве того, что функционал J обладает

первой вариацией в любой точке x*(.) такой, что точки ,

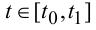, принадлежат области U, и в получении необходимого условия в

терминах первой вариации. Рассмотрим функцию одной переменной

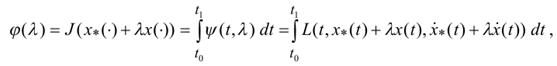(12)

порожденную вариацие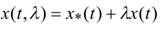й точки 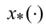по направлению

точки . При наших допущениях относительно L, 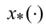и функция является дифференцируемой по l при достаточно малых l, и при этом производная 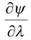непрерывна, так как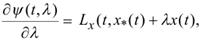

Следовательно, допустимо дифференцирование в (12) под знаком интеграла и при этом

где

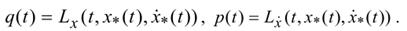Так как исследуемая функция x*(t) допустима, то для любой функции xt (), принадлежащей подпространству =0 }, функция будет проходить через те же граничные точки, что и функция x*(t). Следовательно, если x*(t) есть решение задачи (11), то при условии, , функция, определяемая соотношением (12), должна иметь минимум в точке нуль. В итоге получаем необходимое условие экстремума (13). Первый этап вывода закончен.

Второй этап состоит в преобразовании выражения для первой вариации на пространстве L0 посредством интегрирования по частям. Делают это двумя способами: следуя Лагранжу, когда интегрируют по частям второе слагаемое, и, следуя Дюбуа-Раймону, когда интегрируют первое слагаемое. Преобразование по Лагранжу предполагает дополнительное условие гладкости, а именно, допущение, что функция является непрерывно дифференцируемой. При этом дополнительном предположении проинтегрируем по частям второе слагаемое в выражении для первой вариации при условии, что 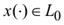. Получим:

Приведем теперь преобразование первой вариации по Дюбуа-Раймону. Для этого проинтегрируем по частям первое слагаемое на пространстве L0:

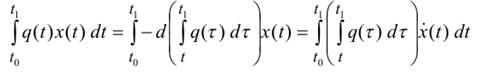
и получим, что выражение для первой вариации имеет следующий вид:

Переходим к третьему этапу вывода уравнения Эйлера.

Лемма 1 (Лагранжа). Пусть функция a(t) непрерывна на отрезке [t0,t1]. Предположим, что для любой непрерывно дифференцируемой функции x(t),обращающейся в нуль на концах отрезка [t0,t1], выполнено равенство

тогда a(t) = 0.

Лемма 2 (Дюбуа-Раймона). Пусть функция b(t) непрерывна на отрезке [t0,t1]. Предположим, что для любой непрерывной функции v(t), в среднем равной нулю, выполнено равенство

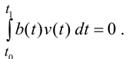Тогда b(t) = b0 = const.

Следствие 1. Пусть в задаче (11) лагранжиан L непрерывно дифференцируем в некоторой области такой, что ей принадлежат точки . Для того чтобы функция x*(t) доставляла слабый локальный минимум в задаче (11), необходимо, чтобы было выполнено уравнение Эйлера в форме Лагранжа:

(16). Функции x*(t), вдоль которых выполнено уравнение Эйлера, называются экстремалями. Приведем несколько частных случаев, когда у уравнения Эйлера имеются интегралы.

Следствие 2. Если функция L не зависит от x, то для экстремальности x*(t) необходимо, чтобы было выполнено соотношение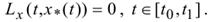

Следствие 3. Если функция L не зависит от x, то уравнение Эйлера допускает интеграл импульса:

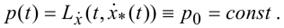
Следствие 4. Если функция L не зависит от t, то уравнение Эйлера допускает интеграл энергии:

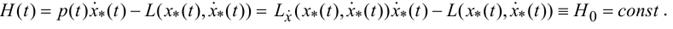Следствия 1 и 2 непосредственно вытекают из (16). Для доказательства следствия 3 надо взять производную и, воспользовавшись (16), показать, что она равна нулю.

Не нашли, что искали? Воспользуйтесь поиском: