Симметрия кристаллов

Поразительное свойство кристаллов состоит в их характерной форме с плоскими поверхностями. Например, кристаллы каменной соли (NaCl) имеют форму прямоугольных параллелепипедов с одинаковыми гранями. Эти кристаллы имеют высокую степень симметрии. Определённая внешняя форма является исключительно проявлением внутренней структуры кристаллов. Открытие дифракции рентгеновских лучей на кристаллах Лауэ в 1912г. позволило подтвердить это предположение и начать конкретное изучение структуры кристаллов.

Рентгеновские исследования по дифракционным картинам позволили установить, что расположение атомов и молекул подчиняются определённому правилу, вытекающему из свойств симметрии кристаллов: они образуют так называемую кристаллическую решётку.

В простейших случаях во всех её узлах находятся одни и те же атомы или молекулы. В каждом из направлений они находятся друг от друга на определённом расстоянии. Идеальный кристалл можно построить путём бесконечного закономерного повторения в пространстве одинаковых структурных единиц.

Решётка Браве. При описании любого кристаллического тела используется фундаментальное понятие решётки Браве, которое характеризует периодическую структуру, образуемую повторяющимися элементами кристалла. Фактически понятие решётки Браве находит своё отражение только в геометрии кристалла. Введение этого понятия предполагает, что для описания тела, состоящего из атомов расположенных в пространстве регулярным образом можно ввести три некомпланарных вектора основных трансляций обладающих следующими свойствами. При рассмотрении решётки из произвольной точки r, решётка имеет тот же вид, что и при рассмотрении из точки

,

где целые положительные числа. Часто основные векторы трансляций обозначают через векторы Совокупность точек при различных наборах чисел {n}определяет кристаллическую решётку, представляющую собой регулярное периодическое расположение точек в пространстве. Кристаллическая структура образуется лишь тогда, когда с каждой точкой решётки будет связан базис, т.е. начинка её из атомов, молекул и т.д. Во многих кристаллах металлов базис состоит из одного атома, но известны неорганические и биологические структуры, базис которых содержит тысячу и более атомов.

Вершины параллелепипедов, построенных на базисных векторах { a }-называются узлами Браве, а решётка, образованная этими узлами, решёткой Браве. Узлы решётки Браве в общем случае не являются узлами кристаллической решётки, т.е. местом расположения атомов или ионов. Действительно, в общем случае при построении решётки Браве в качестве нулевого узла можно выбрать произвольную точку кристалла r, поэтому остальные узлы Браве могут попасть в произвольные, но эквивалентные точки . Эквивалентными точками в кристалле называются такие точки, которые по всем геометрическим и физическим свойствам неотличимы друг от друга.

Точки решётки Браве, лежащие ближе всего к данной точке называются ближайшими соседями. В силу периодичности решётеи Браве, любая точка имеет одинаковое число ближайших соседей. Поэтому это число является характеристикой решётки и его называют коородинационным числом этой решётки.

Параллелепипед, построенный на базисных векторах, называется примитивной ячейкой - частный случай элементарной ячейки.

С помощью соответствующих трансляций элементарной ячейки можно заполнить всё пространство кристаллической структурой. Примитивная ячейка имеет минимальный объём. Это обеспечивается выбором основных векторов, который в общем случае является неоднозначным. На примитивную ячейку приходится только один узел кристаллической решётки. Если на элементарную ячейку приходится один узел, то удобно совместить узлы решётки с местоположением атомов и тогда решётка Браве совпадёт с реальной кристаллической решёткой. Недостаток такого выбора примитивной ячейки заключается в том, что он не отражает полной симметрии решётки Браве. Например, рассмотрим кристаллическую структуру с гранецентрированной решёткой (ГЦК) Браве. Для неё тройку базисных векторов можно выбрать в виде

,

где i ,j,k– базисные векторы декартовой системы координат, a – длина ребра куба. В этом случае любой узел решётки Браве в математической форме может бытьописан с помощью вектора

,

где – целые положительные и отрицательные числа, включая и нуль. Косой параллелепипед, построенный на этих базисных векторах (см. рис.) не обладает полной кубической симметрией.

На этом рисунке большой куб – условная элементарная ячейка. Заштрихованный параллелепипед – примитивная ячейка. Она имеет объём равный четверти объёма куба и имеет более низкую симметрию. Для решения задачи выбора элементарной ячейки кристалла имеющей симметрию данной кристаллической решётки имеется метод, предложенный Вигнером и Зейтцем. Его рассмотрение мы проведём несколько позднее.

Если же на элементарную ячейку приходится несколько атомов, то за нулевой узел решётки Браве можно выбрать место положения одного из них. Поэтому число узлов решётки Браве будет меньше числа узлов кристаллической решётки, тогда с остальными атомами следует связать ещё решётки Браве и тем самым получить сложную кристаллическую структуру с несколькими взаимопроникающими решётками Браве. Решётки, построенные таким образом, называются прямыми решётками.

Граничные условия Борна-Кармана. Поскольку все точки решётки Браве эквивалентны, она должна иметь бесконечную протяжённость. Но так как реальные кристаллы всегда конечны, то чтобы корректно описывать кристаллы на языке кристаллических структур необходимо делать некоторые предположения. Во-первых, предполагается, что кристалл имеет достаточно большие размеры, чтобы можно было пренебречь влиянием атомов, расположенных на поверхности на объёмные свойства кристалла. Действительно, погрешность такого приближения оценивается как отношение числа атомов на поверхности к числу атомов в объёме 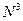, т.е. равна - где - число атомов в кристалле. Это физическое предположение. С математической точки зрения данное предположение может быть записано в виде периодических граничных условий следующим образом. Обозначим через вектор – вектор трансляции примитивной ячейки

,

где совокупность целых положительных и отрицательных чисел, включая нуль. Теперь переход к конечному кристаллу математически можно осуществить следующим образом. Введём в каждом из трёх направлений, определяемых базисными векторами число ячеек тогда полное число ячеек N в конечном кристалле, будет равно . При этом должны выполняться следующие соотношения

Чётность или нечетность величин N значения не имеет, поскольку предполагается, что они имеют очень большие значения. Пусть теперь наш кристалл имеет такие размеры по трём базисным направлениям и . Тогда, периодические граничные условия для некоторой произвольной функции должны иметь вид

, ,

Т.е. фактически требуется отождествление двух противоположных поверхностей кристалла. Такое замыкание противоположных граней кристалла возможно только теоретически. Эти условия принято называть циклическими периодическими граничными условиями Борна - Кармана.

Сингонии.

Решётки Браве обладают определённой симметрией относительно поворотов и отражений. Для каждой решётки Браве существует точечная группа K преобразований, которые переводят вектор решётки в вектор решётки. Ортогональные преобразования трёхмерного пространства, принадлежащие группе K, будем обозначать через . Существует семь систем (сингоний) кристаллических решёток, различающихся точечной группой К. Оказывается, не всякая точечная группа может быть группой симметрии решётки. Требование, чтобы одновременно с a вектор также был вектором решётки, ограничивает круг допустимых точечных групп. Выясним эти ограничения. Прежде всего, следует отметить, что группа K должна содержать инверсию I: вместе с трансляцией на вектор a в группу всегда входит трансляция на вектор – a. Теперь установим, какие оси симметрии может иметь группа K? Выберем в качестве ортов базиса пространства векторов основные векторы решётки и запишем преобразование в новом базисе, в котором все векторы решётки имеют целочисленные составляющие. Если матрицу ортогональных преобразований обозначить через , то мы будем иметь

,

где - матрица перехода от первоначального ортонормированного базиса к базису . Если - поворот (или зеркальный поворот) на угол , то след матрицы , так же как и след матрицы , равен

.

Однако из условия, что преобразование должно переводить целочисленный вектор решётки в целочисленный вектор, следует, что все элементы матрицы , а, следовательно, и её след должны быть целочисленными. Отсюда получаем, что может принимать лишь следующие значения

.

Следовательно, группа K может содержать оси только второго, третьего, четвёртого и шестого порядков. Есть здесь ещё одно ограничение, которое доказыватьне будем. А сразу сформулируем вывод: все ограничения приводят ктому, что роль точечной группы кристалла могут играть лишь семь точечных групп, а именно:

.

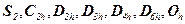Это и является причиной того, что существует только семь сингоний (систем): триклинная, моноклинная, ромбическая, ромбоэдрическая, тетрагональная, гексагональная, кубическая. Перечислим свойства этих точечных групп:

они содержат инверсию;

не содержат осей 5-го, 7-го и более высоких порядков;

вместе с осью 3-го,4-го или 6-го порядков они содержат также и плоскости, проходящие через эти оси.

Рассмотрим теперь векторные группы, принадлежащие одной и той же сингонии.

Точечная группа решётки Бравэ накладывает определённые ограничения на возможное расположение и относительные длины основных векторов решётки.

Две векторные группы, принадлежащие одной и той же сингонии, называются однотипными, если одна из них может быть переведена в другую с помощью непрерывной деформации; при этом в процессе деформации симметрия векторной группы должна быть не ниже, чем симметрия групп данной сингонии. Эти требования, предъявляемые к векторным группам, приводят к тому, что существует только 14 типов векторных групп. Рассмотрим подразделение решёток Браве на системы:

1)В триклинной системе единственная пространственная решётка имеет примитивную (Р) элементарную ячейку, в которой все три базисных вектора имеют разную длину, а все углы не равны между собой.

2) В моноклинной системе имеются две пространственные решётки: одна имеет примитивную (Р) элементарную ячейку, другая (С) имеет элементарную ячейку с центрированными основаниями (в центре оснований располагаются узлы) ячейки, нормальных к вектору

3) В ромбической системе имеется четыре пространственные решётки:

тип P имеет примитивную ячейку, тип С -ячейку с центрированными основаниями, тип I – объёмноцентрированную, т.е. буквально «внутрицентрированную» и, наконец, тип F – гранецентрированную.

4) В тетрагональной системе простейшей ячейкой будет правильная призма с квадратом в основании. Эта ячейка примитивная, и поэтому решётка называется тетрагональной типа Р. Вторая тетрагональная ячейка типа I –объёмноцентрированная.

5) В кубической системе возможны три типа решётки: простая кубическая P с примитивной ячейкой, объёмноцентрированная I кубическая решётка (ОЦК) и гранецентрированная F кубическая решётка (ГЦК).

6) В тригональной системе в качестве элементарной ячейки обычно

выбирают ромбоэдр. Решётка является примитивной, но обозначают её обычно буквой R, а не P, и соответственно называют её тригональной пространственной решёткой типа R.

для того чтобы подчеркнуть принадлежность данной элементарной ячейки к гексагональной системе, часто добавляют к ней ещё две ячейки, повёрнутые друг относительно друга на угол , получая, таким образом, утроенную ячейку в форме гексагональной призмы, имеющей в основании правильный шестиугольник.

Рассмотрим теперь симметрию направлений в кристалле. Совокупность всех поворотов, зеркальных поворотов, которые переводят каждое направление в кристалле в эквивалентное направление, образует точечную группу F, характеризующую симметрию направлений. Элементы этой группы не обязательно принадлежат группе симметрии кристалла, так как от них не требуется, чтобы они переводили все точки кристалла в эквивалентные точки.

Группу F можно охарактеризовать следующим образом. Всякий элемент g группы G кристалла, очевидно можно представлять в виде . Совокупность всех элементов , соответствующих элементам g, образует точечную группу. Эта точечная группа есть не что иное, как группа направлений F. Все кристаллы, имеющие одну и ту же группу направлений, образуют один кристаллический класс. Оказывается, что существует всего 32 группы направлений и, следовательно, 32 кристаллических класса. Каждый элемент группы F является в то же время элементом группы K, т.е. F содержится в K, следовательно, F является подгруппой группы K. Так как у семи групп, характеризующих сингонии, существует ровно 32 подгруппы, то и число различных классов равно 32.

Распределение кристаллических классов между сингониями

Сингонии	Классы
Триклинная…………...
Моноклинная…………
Ромбическая………….. Тетрагональная……….
Ромбоэдрическая……..
Гексагональная………..
Кубическая…………….

До сих пор мы рассматривали симметрию «пустых» решёток. Вернёмся теперь к рассмотрению симметрии кристалла.

Кроме подгруппы трансляций, пространственная группа содержит так же другие преобразования, вид которых обусловлен, во - первых, симметрией решётки Браве, во – вторых, симметрией компонентов кристалла, т. е. симметрией периодически повторяющееся совокупности частиц, образующей кристалл. Это обстоятельство часто приводит к тому, что не все преобразования, совмещающие узлы пустой решётки, совмещают также компоненты кристалла. Поэтому возможно, что точечная группа кристалла будет только подгруппой точечной группы пустой решётки. Вследствие этого, в группу симметрии кристалла необходимо, кроме целочисленных трансляций ввести и нецелочисленные трансляции. Тогда общий элемент пространственной группы следует представлять в виде , где - некоторые преобразования из точечной группы K, а - трансляции на вектор , отличный от вектора решётки. Для пояснения таких несобственных трансляций рассмотрим кристаллическую решётку алмаза. Её можно составить из двух гранецентрированных кубических решёток, сдвинутых друг относительно друга вдоль пространственной диагонали куба на ¼ её длины, при этом , где a -постоянная решётки (длина ребра куба).

Пространственные группы делятся ещё на симморфные и несимморфные. Симморфными называются такие группы, в которых после каждой операции симметрии из точечной группы F осуществляется трансляция на вектор решётки. Несимморфными группами являются группы с нецелочисленными трансляциями. Всего существует 230 пространственных групп. Эти 230 групп называют федоровскими по имени российского кристаллографа Фёдорова, открывшего их. Из них симморфными являются 73 группы, остальные несимморфные.

Не нашли, что искали? Воспользуйтесь поиском: