Изоморфизм и гомоморфизм групп

Группы 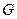и между элементами, которых существует взаимнооднозначное соответствие, не нарушающееся при групповом умножении, называются изоморфными. Установление изоморфизма позволяет свести исследование одной группы к рассмотрению другой, изоморфной ей. Изоморфные группы имеют одинаковую структуру.

Другим важным понятием в теории групп является понятие гомоморфизма. Если каждому элементу группы 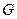соответствует только один определённый элемент группы,G, а каждому элементу группы соответствует несколько элементов группы 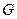, причём это соответствие сохраняется при групповом умножении, то говорят, что группа гомоморфна группе 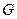. Гомоморфные группы обладают следующими свойствами:

1.Если группа гомоморфна группе 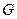, то единичному элементу группы G соответствует единичный элемент группы .

2. Если группа гомоморфна группе 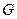, то взаимно обратным элементам группы 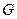соответствуют взаимно обратные элементы группы .

3. Если группа гомоморфна группе 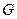, то все элементы группы 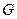, соответствующие единичному элементу , образуют инвариантную подгруппу N группы G.

Не нашли, что искали? Воспользуйтесь поиском: