Регулярное представление

Пусть задана группа G. Возьмём произвольный её элемент 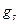и произведём операцию левого сдвига по группе, т.е. каждый элемент группы умножим слева на 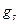. Тогда как мы знаем из §2, если то ни один элемент группы не останется на месте. Если же то никакого сдвига не произойдёт. Сдвиг, соответствующий любому элементу 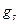, можно формально записать с помощью матрицы порядка m:

.

Очевидно, что в каждом столбце матрицы R имеется только один элемент отличный от нуля и равный единице. Если 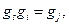то а , если . Матрицы, построенные таким образом, дают представление порядка m группы G, которое называется регулярным.

Из определения регулярного представления следует, что его характеры таковы:

если

если

Разложим регулярное представление на неприводимые части, т. е. выясним, сколько раз в нём содержится каждое неприводимое представление . Для этой цели нам следует найти величину . По известной формуле для неё, получаем

Или, согласно последним формулам для характеров регулярного представления

Таким образом, мы видим, что каждое неприводимое представление содержится в регулярном представлении столько же раз, каков порядок этого неприводимого представления.

С помощью этой теоремы мы можем выразить порядок регулярного представления через порядки неприводимых представлений, на которые оно распадается. Вот это выражение

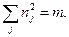
В заключение этого параграфа без доказательства сформулируем ещё одну теорему: число различных неприводимых представлений группы равно числу её классов сопряжённых элементов.

На основании теоремы о произведении двух классов сопряжённых элементов нетрудно получить основную формулу для вычисления характеров неприводимых представлений:

,

где - число элементов в классе p -номер неприводимого представления, 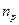- его размерность. На основании выше изложенного, можно сделать такой вывод: поскольку в циклической группе каждый элемент группы сам по себе образует класс, значит, число представлений в этой группе равно числу её элементов и каждое представление имеет размерность равную единице.

Не нашли, что искали? Воспользуйтесь поиском: