Представления групп

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Наиболее существенные применения, которые нашла себе теория групп в физике, ими оказывается в подавляющем большинстве один из разделов теории групп, именно, теория представлений.

Теория представлений изучает гомоморфные отображения произвольной группы на всевозможные группы линейных операторов. Значение теории представлений связано с тем обстоятельством, что подобные отображения возникают «сами собой», при рассмотрении задач, обладающих той или иной симметрией.

Определение представления. Мы будем говорить, что задано представление T группы G в некотором линейном пространстве L, если каждому элементу g группы G отвечает линейный оператор T (g) в пространстве L так, что при этом произведению элементов группы отвечает произведение операторов, т. е.

Размерность пространства L называют размерностью представления. Группа может иметь представления как конечномерные, так и бесконечномерные. Здесь мы будем изучать только первые.

Рассмотрим векторное пространство над полем комплексных чисел. Пусть каждым двум векторам из L, заданным в определённом порядке, отнесено некоторое комплексное число, называемое скалярным произведением этих векторов и обозначаемое через (xy) или (x,y). Пусть при этом имеют место следующие свойства скалярного умножения.

Для любых x, y, z из L и любого комплексного числа имеют место соотношения

1. (x,y)=(y,x)*,

2. ( x,y)= (x,y),

3. (x+y,z)=(x,z)+(y,z),

В этом случае говорят, что в пространство L внесена эрмитова метрика. Если же имеет место такое соотношение (x,x)>0 и чтобы , то эрмитова метрика называется положительно определённой. Звёздочка, поставленная в правой части соотношения (1) обозначает коплексное сопряжение.

Эквивалентные представления. Одна из задач теории представлений состоит в перечислении всех возможных представлений данной группы. При решении этой задачи существенную роль играют два понятия: понятие эквивалентности представлений и понятие приводимости представлений. Рассмотрим сначала эквивалентность.

Если известно какое-либо представление 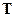группы в пространстве L, то нетрудно построить сколь угодно новых представлений группы. Для этого следует выбрать какой - либо неособенный оператор A, переводящий векторы из пространства, L в какое – либо пространство того же числа измерений (в частности, L может совпадать с L) и сопоставить элементу вместо оператора оператор , действующий в пространстве . Нетрудно проверить, что соответствие определяет представление группы. Всякие два представления группы, связанные оператором A называются эквивалентными. Все представления эквивалентные данному представлению эквивалентны между собой. Поэтому все представления группы распадаются на классы взаимно- эквивалентных представлений. Если известно хотя бы одно представление из этого класса, то любое другое представление их этого же класса может быть получено без труда.

Тем самым задача нахождения всех представлений сводится к более узкой задаче нахождения всех взаимно-неэквивалентных представлений. Так как из каждого класса эквивалентных представлений достаточно выбрать для дальнейшего изучения только по одному представителю, то желательно сделать этот выбор более рациональным образом. В настоящем конспекте будем рассматривать только те группы, у которых каждое представление эквивалентно некоторому унитарному представлению.

Дадим определение: векторное линейное пространство, заданное над полем комплексных чисел и с эрмитовой метрикой называется унитарным. Операторы же определённые в этом пространстве и называются унитарными.

Можно сформулировать и доказать такую теорему: каждый класс эквивалентных представлений конечной группы содержит унитарные представления.

Введение понятия унитарных представлений позволяет свести задачу перечисления всех представлений к нахождению только неэквивалентных представлений. Однако, эту задачу можно ещё сузить если ввести понятие приводимых и неприводимых представлений. Обсудим эти представления.

Представление 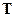группы G в пространстве L называется приводимым, если в L существует хотя бы одно нетривиальное подпространство , инвариантное относительно всех операторов . Напомним, что подпространство линейного пространства L называется инвариантным относительно некоторого оператора А, если этот оператор, действуя на векторы , переводит их в векторы, принадлежащие этому же подпространству, т.е. .

Все подпространства пространства L, кроме самого L и нуль - пространства называются нетривиальными.

В соответствии с этим представление 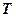группы G в пространстве L называется неприводимым, если в L не существует ни одного нетривиального подпространства , инвариантного относительно всех операторов T (g).

Ценность существования неприводимых представлений определяется следующей теоремой: Пусть 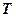унитарное приводимое представление группы G в пространстве L, а - инвариантное подпространство. Тогда ортогональное дополнение к - подпространство - инвариантно. В результате применения этой теоремы вытекает следующее: если пространство L преобразуется по некоторому приводимому унитарному представлению, то оно расщепляется на два взаимно ортогональных инвариантных подпространства и , т.е.

L = + .

В каждом из этих подпространств реализуются свои представления и соответственно. Эти два представления называются индуцированными. Таким образом, приводимое представление расщепляется на два неприводимых представления.

Если хотя бы одно из этих двух представлений приводимо, то его можно в свою очередь разбить на два представления меньшей размерности. Продолжая этот процесс, мы неизбежно придём к неприводимым представлениям, если исходное приводимое представление было конечным. Пространство L при этом окажется разложенным на сумму взаимно - ортогональных подпространств

Представление Т можно называть суммой неприводимых представлений.

Если в качестве базисных векторов в пространстве L взять совокупность базисных векторов инвариантных подпространств, то матрицы, соответствующие операторам Т ( g) примут квазидиагональный вид. Приведём здесь без доказательства одно из важнейших свойств матричных элементов различных неприводимых представлений - это свойство называется свойством ортогональности. Пусть и -матрицы двух неэквивалентных неприводимых представлений группы G порядка m. Обозначим через и размерности матриц этих представлений. Тогда можно доказать (опираясь на некоторые дополнительные леммы) следующие соотношения ортогональности.

Звёздочка в формулах обозначает комплексное сопряжение.

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: