Тема 15. Теорія ймовірностей 1 страница

Варіант 1

1. Гральна кісточка підкидається один раз. Результат експерименту – число очок на верхній грані. Розглянемо події: 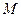– випала четвірка; 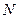– випало менше ніж три очки; 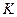– випала непарна кількість очок. Які з даних подій сумісні, а які – ні? Описати події: .

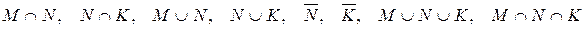2. Учасники жеребкування тягнуть із ящика жетони з номерами від 1 до 100. Знайти ймовірність того, що номер першого навмання взятого жетона не містить цифри 3.

3. Н одній доріжці магнітофонної стрічки довжиною 200м записане повідомлення на проміжку 20м, на другій – записано аналогічне повідомлення. Знайти ймовірність того, що на інтервалі від 60 до 85м не буде проміжку стрічки, який не містить запису, якщо початки обох повідомлень рівно можливі в будь-якій точці від 0 до 180м.

4 Підкидають гральну кісточку два рази підряд. Яка ймовірність того що: а) обидва рази випаде парне число очок; б) обидва рази випаде непарне число очок; в) сума очок, які випали ділиться (кратна двом) на два; г) сума очок, які випали дорівнює 11?

5. З двох станків на загальний конвеєр поступають деталі. Ймовірність виготовлення нестандартної деталі для першого станка дорівнює 0,02, для другого – 0,03. Швидкість першого станка у два рази більша від швидкості другого. Яка ймовірність взяти якісну (стандартну) деталь із загального конвеєра?

6. Ймовірність сходу зерна ярого жита даної партії дорівнює 0,7. Яка ймовірність того, що із 100 висіяних зернин цієї партії зійде від 70 до 80 насінин?

7. Знайти числові характеристики розподілу дискретної випадкової величини, яка задана законом розподілу

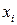
	0,2	0,8	2,6	3,4
	0,1	0,4	0,2	0,3

8. Неперервна випадкова величина задана показниковим розподілом

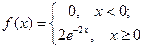
Знайти числові характеристики цього розподілу.

9. Система випадкових величин 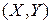на всій площині має щільність

.

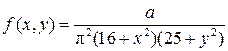Знайти: а) сталу 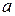; б) інтегральну функцію .

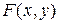Варіант 2

1. Підкидають три монети. Розглянемо події: 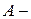випало принаймні 2 герби; 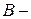на першій монеті випав герб; 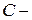випала хоча б одна цифра. Які з даних подій сумісні, а які – ні? Описати події:

.

2. Випадково відібрана кісточка доміно виявилась не дублем. Знайти ймовірність того, що другу навмання взяту кісточку доміно можна прикласти до першої.

3. В точці 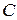, положення якої на телефонній лінії 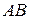довжиною 20км, рівно можливе, відбувся розрив. Визначити ймовірність того, що точка 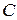віддалена від точки на віддалі, яка не менша 15км.

4. Підкидають гральну кісточку один раз. Яка ймовірність того що: а) випаде парне число очок; б) випаде непарне число очок; в) випало число очок кратне трьом: г) випаде сім очок?

5. З двох станків на загальний конвеєр поступають деталі. Перший станок дає 5% бракованих деталей, другий – 3%. Швидкість першого станка у два рази більша від швидкості другого. Яка ймовірність взяти нестандартну деталь із загального конвеєра?

6. Ймовірність народження хлопчика 0,52. Яка ймовірність того, що в сім’ї із 5 дітей рівно 3 хлопчики?

7. Записати закон розподілу дискретної випадкової величини Х – числа гербів які випали при двох підкиданнях монети.

8. Неперервна випадкова величина задана нормальним законом розподілу із параметрами , 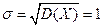. Знайти числові характеристики цього розподілу та ймовірність попадання випадкової величини в інтервал (0; 1).

9. Координати 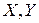випадкової точки розподілені рівномірно всередині прямокутника, обмеженого абсцисами 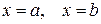і ординатами 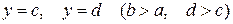. Знайти густину ймовірності і функцію розподілу системи величин .

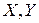Варіант 3

1. Гральна кісточка підкидається один раз. Результат експерименту – число очок на верхній грані. Розглянемо події: 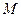– випало більше ніж 3 очки; 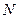– випало менше ніж 5 очок; 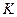– випало число 3. Які з даних подій сумісні, а які – ні? Описати події: .

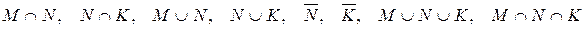2. Куб всі грані якого пофарбовані розрізали на 27 однакових кубиків. Одержані кубики добре перемішують. Знайти ймовірність того, що навмання взяті два кубики мають пофарбовані грані.

3. Супутник Землі рухається за орбітою, яка знаходиться між 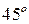північної та 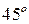південної широти. Вважаючи однаково можливим падіння супутника в будь-яку точку поверхні Землі між вказаними паралелями, знайти ймовірність того, що супутник впаде вище 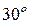північної широти.

4. Підкидають монету три рази підряд. Яка ймовірність того що: а) всі рази випаде герб; б) випаде два рази герб; в) герб не випаде ні одного разу; г) герб випаде один раз?

5. В секретному замку 5 дисків, які поділені на 10 пронумерованих секторів від 0 до 9. Яка ймовірність відкрити замок з першого разу при довільному наборі цифр на дисках?

6. Ймовірність влучення у ціль при одному пострілі 0,8. Яка ймовірність влучити у ціль 70 разів при 100 пострілах?

7. На складі 10 всіх колінчатих валів, серед яких 2 неякісних. Наугад взяли 3 вали. Записати закон розподілу дискретної випадкової величини Х – числа неякісних валів серед відібраних.

8. Автобуси деякого маршруту їздять строго за графіком з інтервалом 10хв. Знайти ймовірність того, що пасажир, який підійшов на зупинку, буде чекати наступний автобус не більше 3хв.

9. Знайти закони розподілу складових дискретної двомірної випадкової величини, яка задана законом розподілу

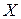
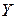
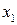
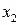
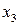
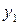
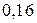
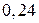
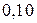
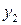
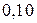
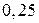
Варіант 4

1. Гральна кісточка підкидається два рази. Результат експерименту – сума очок, що випали. Розглянемо події: 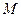– сума очок рівна 3; 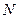– сума очок, що випали менша 11; 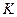– сума очок ділиться на 5. Які з даних подій сумісні, а які – ні? Описати події:

.

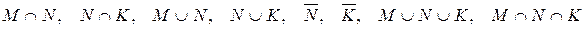2. З повного набору кісток доміно беруть 7 штук. Яка ймовірність того, що серед них буде хоча б одна з шістьма очками.

3. Після бурі на ділянці 50-м і 80-м кілометрами лінії електропередач стався обрив проводу. Яка ймовірність того, що цей розрив стався між 50-м та 60-м кілометрами лінії?

4. З колоди у 36 карт витягують дві підряд. Яка ймовірність того що: а) обидва рази витягли туза; б) обидва рази витягли чорну карту; в) сума очок, які витягли дорівнює 21 (очко); г) обидва рази витягли кольорову карту?

5. В трьох ящиках є яблука чотирьох сортів: А «Апорт»; Б «Білий налив»; Р «Ранет»; С «Слава переможцю» відповідно у кількостях: у першому А – 20%; Б – 40%; Р – 30%; С – 10%; у другому А – 20%; Б – 30%; Р – 30%; С – 20%; у третьому А – 10%; Б – 50%; Р – 20%; С – 20%. З наугад взятого ящика взяли яблуко. Яка ймовірність того, що це яблуко відноситься до групи Б?

6. Ймовірність сходу зерна ярого жита даної партії дорівнює 0,7. Яка ймовірність того, що із 100 висіяних зернин цієї партії зійде рівно 70 насінин?

7. Знайти числові характеристики розподілу дискретної випадкової величини, яка задана законом розподілу

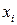
	0,1	0,4	0,2	0,3

8. Неперервна випадкова величина задана показниковим розподілом

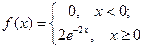
Знайти ймовірність того, що випадкова величина попаде у інтервал (0; 1).

9. Задана диференціальна функція двомірної випадкової величини

.

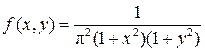Знайти ймовірність попадання випадкової точки в прямокутник з вершинами .

Варіант 5

1. Гральна кісточка підкидається один раз. Результат експерименту – число очок на верхній грані. Розглянемо події: 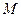– випала п’ятірка; 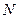– випало не менше ніж 2 очок; 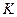– випала парна кількість очок. Які з даних подій сумісні, а які – ні? Описати події: .

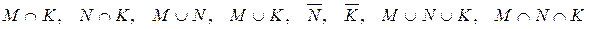2. Із повного набору кісток доміно (28) навмання беруть одну. Яка ймовірність того, що сума очок на ній дорівнює 7?

3. Екран осциляційного лічильника, що має форму квадрата зі стороною 10см, бомбардується частинками. Знайти ймовірність того, що віддаль від точки спалаху: а) до фіксованої сторони квадрата не перевищує 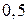; б) до найближчої сторони не перевищує .

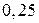4. Підкидають гральну кісточку один раз. Яка ймовірність того що: а) випаде три очоки; б) випаде непарне число очок; в) випало число очок кратне чотирьом: г) випаде нуль очок?

5. На складі є 15 підшипників, серед яких 3 мають дефект у прихованому вигляді. Складальник наугад взяв 2 підшипники. Яка ймовірність того, що один із них із дефектом?

6. Ймовірність влучення у ціль кожним із трьох мисливців відповідно рівна: 0,6; 0,7; 0,8. Яка ймовірність двох влучень при одному залпі?

7. Записати закон розподілу дискретної випадкової величини Х – числа випавших одиниць при трьох підкиданнях гральної кісточки.

8. Знайти середню вибірки та побудувати полігон частот

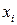
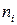
9. Знайти ймовірність попадання випадкової точки 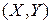в прямокутник, який обмежений прямими 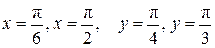. Відома інтегральна функція .

Варіант 6

1. З колоди в 36 карт навмання витягують одну. Розглянемо події: 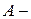витягнули карту червоної масті; 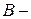витягнули короля; 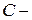витягнули даму треф. Які з даних подій сумісні, а які – ні? Описати події:

.

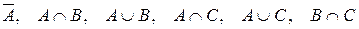2. Відомо, що високосний рік має 52 тижні і 2 дні. Яка ймовірність того, що у вибраному навмання високосному році буде 53 неділі?

3. Двоє друзів відвідують одну і ту ж кав’ярню між 11 та 12 годиною. Кожен з них приходить у випадковий момент даного проміжку, 10 хвилин п’є каву і йде геть. Яка ймовірність зустрітись друзям випадково?

4. Підкидають монету два рази підряд. Яка ймовірність того що: а) два рази випаде герб; б) жодного разу не випаде герб; в) герб випаде один раз?

5. В ящику 5 пронумерованих кубиків. По одному виймають всі кубики. Яка ймовірність того, що номера вийнятих кубиків з’являться у зростаючому порядку?

6. Ймовірність влучення у ціль при одному пострілі 0,6. Яка ймовірність влучити у ціль 80 разів при 100 пострілах?

7. Три поліграфічні фірми виготовляють бланки бухгалтерських документів: перша 30%, друга – 40%, третя – решту. Ймовірність неякісного виготовлення документа для першої фірми дорівнює 0,001, для другої – 0,002, для третьої – 0,003. Яка ймовірність придбати неякісний документ споживачу?

8. Знайти ймовірність попадання нормально розподіленої випадкової величини у інтервал (0; 5) з параметрами , .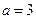

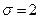9. Знайти диференціальну функцію системи випадкових величин за відомою інтегральною функцією .

Варіант 7

1. Три рази стріляють в мішень. Розглянемо події: 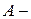принаймні два влучення; 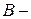влучення у першому пострілі; 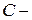хоча б один промах. Які з даних подій сумісні, а які – ні? Описати події:

.

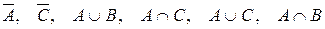2. Із слова «ймовірність» вибирається одна буква. Яка ймовірність того, що це буде буква «О»? Яка ймовірність того, що це голосна?

3. Знайти ймовірність того, що навмання взята точка в крузі радіусом 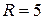см, попаде в круг радіусом см, який міститься в заданому?

4. Робітник обслуговує три автоматичні станки. Нехай А ₁, А ₂, А ₃ – події, які полягають у тому, що відповідно перший, другий та третій станки потребують уваги робітника протягом години. Що означають події:

а) А ₁ А ₂ А ₃, б) А ₁ +А ₂ +А ₃, в) ,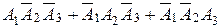

г) ,

5. Є три однакові коробки. У першій коробці 10 білих і 5 чорних кульок, у другій – 8 білих і 8 чорних кульок, а в третій – 2 зелені і 4 чорні. Навмання вибирається коробка і кулька в ній. Знайти ймовірність того, що:

а) взята кулька біла; б) взята кулька чорна.

6. Монету підкинули 8 разів. Яка ймовірність того, що герб випаде 3 рази?

7. Мисливець стріляє в дичину до першого влучення, але встигає зробити не більше чотирьох пострілів. Скласти закон розподілу числа пострілів, якщо ймовірність влучення при одному пострілі рівна 0,7.

8. Побудувати полігон частот та емпіричну функцію розподілу вибірки; знайти вибіркові середню та дисперсію; визначити моду і медіану та середнє лінійне відхилення статистичного розподілу:

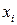
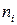
9. Знайти інтегральну функцію розподілу двомірної випадкової величини за заданою диференціальною функцією

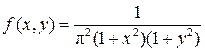, яка задана на всій площині.

Варіант 8

1. Гральна кісточка підкидається два рази. Результат експерименту – число очок, що випали. Розглянемо події: 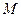– два рази випало парне число очок; 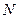– ні разу не випало 4; 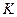– два рази випало число очок, більше 4; 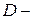принаймні один раз випало парне число очок. Які з даних подій сумісні, а які – ні? Описати події:

.

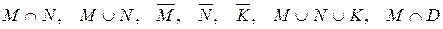2. В ліфт семиповерхового будинку на першому поверсі зайшли три особи. Кожен із них з однаковою ймовірністю виходить на будь-якому поверсі починаючи з другого. Знайти ймовірність того, що всі пасажири вийдуть на четвертому поверсі.

3. Знайти ймовірність того, що точка, взята в крузі радіусом 1см попаде всередину квадрата, вписаного в цей круг.

4. Підкидають гральну кісточку один раз. Яка ймовірність того що: а) випаде три очки; б) випаде непарне число очок; в) випало число очок кратне чотирьом: г) випаде нуль очок?

5. На складі є 10 телевізорів, серед яких 2 мають дефект у прихованому вигляді. Підприємство закупило наугад 3 телевізори. Яка ймовірність того, що один із них із дефектом?

6. Ймовірність влучення у ціль кожним із трьох мисливців відповідно рівна: 0,3; 0,5; 0,8. Яка ймовірність хоча би двох влучень при одному залпі?

7. Записати закон розподілу дискретної випадкової величини Х – числа появи шести очок при трьох підкиданнях гральної кісточки.

8. Знайти середню вибірки та дисперсію розподілу

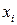
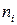
9. Двовимірна випадкова величина 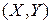задана диференціальною функцією

.

Знайти диференціальні функції складових.

Варіант 9

1. Гральна кісточка підкидається один раз. Результат експерименту – число очок на верхній грані. Розглянемо події: 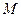– випала шістка; 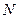– випало не менше ніж 2 очок; 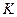– випала непарна кількість очок. Які з даних подій сумісні, а які – ні? Описати події: .

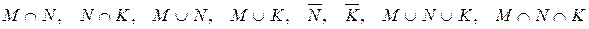2. В ліфт восьмиповерхового будинку на першому поверсі зайшли три особи. Кожен із них з однаковою ймовірністю виходить на будь-якому поверсі починаючи з другого. Знайти ймовірність того, що всі пасажири вийдуть одночасно.

3. Знайти ймовірність того, що навмання взята точка в крузі радіусом 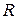попаде всередину рівностороннього трикутника, вписаного в цей круг.

4. Підкидають монету два рази підряд. Яка ймовірність того що: а) два рази випаде герб; б) жодного разу не випаде герб; в) герб випаде один раз?

5. В ящику 6 пронумерованих кубиків. По одному виймають всі кубики. Яка ймовірність того, що номера вийнятих кубиків з’являться у зростаючому порядку?

6. Ймовірність влучення у ціль при одному пострілі 0,8. Яка ймовірність влучити у ціль 80 разів при 100 пострілах?

7. Три поліграфічні фірми виготовляють бланки бухгалтерських документів: перша 30%, друга – 40%, третя – решту. Ймовірність неякісного виготовлення документа для першої фірми дорівнює 0,002, для другої – 0,002, для третьої – 0,003. Яка ймовірність придбати неякісний документ споживачу?

8. Знайти ймовірність попадання нормально розподіленої випадкової величини у інтервал (0; 5) з параметрами , .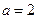

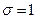9. Двомірна випадкова величина задана таблицею

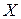
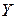
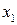
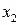
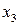
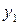
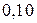
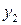
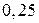
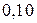
Знайти умовний закон розподілу складової 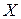при умові, що складова 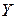прийняла значення .

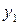Варіант 10

1. Гральна кісточка підкидається два рази. Результат експерименту – пара чисел 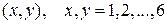. Розглянемо події: – сума чисел, що випали, парна; 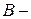випало дві четвірки; 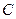– принаймні одне число непарне. Які з даних подій сумісні, а які – ні? Описати події:

.

2. В ліфт восьмиповерхового будинку на першому поверсі зайшли три особи. Кожен із них з однаковою ймовірністю виходить на будь-якому поверсі починаючи з другого. Знайти ймовірність того, що всі пасажири вийдуть на різних поверхах.

3. На паркет складений із рівносторонніх трикутників зі стороною 10см впала монета радіусом 1см. Яка ймовірність того, що монета не перетне жодної із сторін трикутника.

4. В ящику 25 деталей, із них 10 пофарбованих. Яка ймовірність вийняти з ящика пофарбовану деталь?

5. Два станки штампують деталі, які надходять на загальний конвеєр. Ймовірність виготовлення нестандартної деталі першим станком 0,075, другим – 0,09. Продуктивність першого станка вдвоє менша, ніж другого. Знайти ймовірність того, що навмання взята з конвеєра деталь нестандартна.

6. Монету підкинули 6 разів. Знайти ймовірність того, що герб випаде:

а) менше ніж 2 рази; б) не менше двох разів.

7. Записати закон розподілу дискретної випадкової величини Х – числа очок, які випали при підкиданні гральної кісточки, та знайти математичне сподівання цього розподілу.

8. Знайти математичне сподівання і дисперсію розподілу:

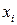
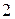
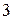
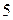
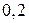
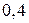
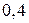
9. Двомірна випадкова величина 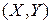задана диференціальною функцією

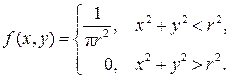
Знайти умовні диференціальні закони розподілу складових.

Варіант 11

1. Гральна кісточка підкидається один раз. Результат експерименту – число очок на верхній грані. Розглянемо події: 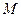– випало не більше ніж 3 очки; 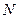– випало не менше ніж 3 очок; 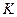– випало більше ніж 5 очок. Які з даних подій сумісні, а які – ні? Описати події: .

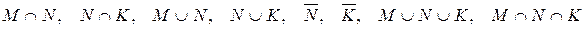2. Батько видає синові щотижня 70грн., а син їх повністю витрачає, причому всі можливі розподіли витрат на кожен день рівно можливі. Знайти ймовірність того, що протягом заданого тижня син витрачатиме по 10грн. в день.

3. Знайти ймовірність того, що точка, взята в крузі радіусом 20см попаде всередину правильного шестикутника, вписаного в цей круг.

4. У колоді 36 карт. Наугад виймають із колоди дві карти по одній. Знайти ймовірність того, що другим буде вийнятий туз, якщо першим був витягнутий: а) туз; б) король.

Не нашли, что искали? Воспользуйтесь поиском: