Уравнение плоскости по трем точкам. Взаимное расположение плоскостей в пространстве

В векторном виде

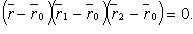
В координатах

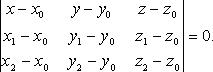
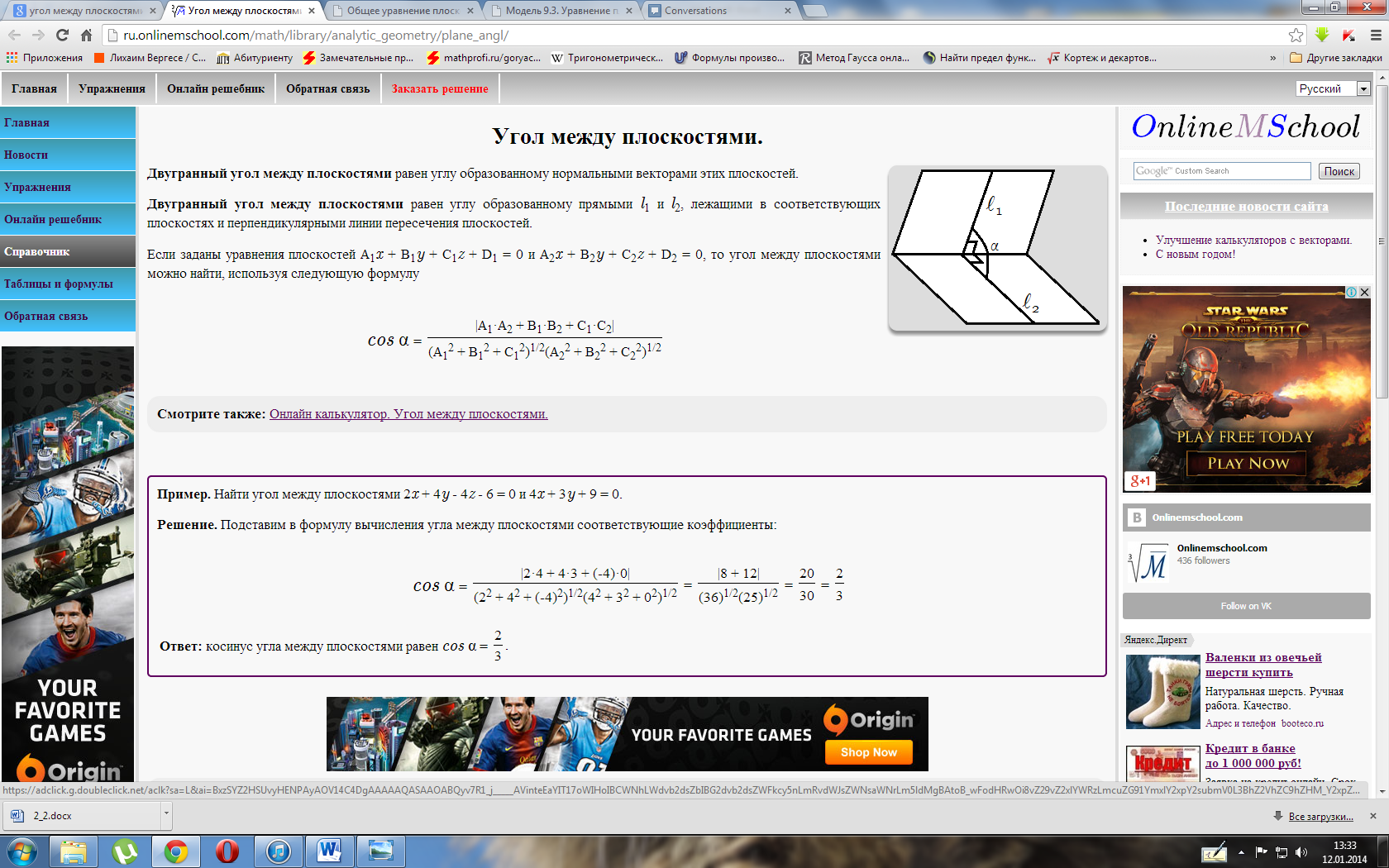
Взаимное расположение плоскостей в пространстве

Пусть

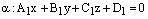и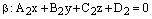

– общие уравнения двух плоскостей. Тогда:

1) если 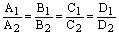, то плоскости совпадают;

2) если 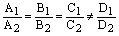, то плоскости параллельны;

3) если или , то плоскости пересекаются и системауравнений

(6)

является уравнениями прямой пересечения данных плоскостей.

3.3

· Составить канонические уравнения прямой по точке и направляющему вектору Решение: Канонические уравнения прямой составим по формуле: Ответ:

· В ряде задач требуется найти какую-нибудь другую точку , принадлежащую данной прямой. Как это сделать? Берём полученные уравнения и мысленно «отщипываем», например, левый кусочек: . Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице: . Так как , то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему: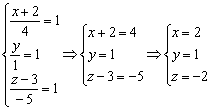

Составить параметрические уравнения следующих прямых:

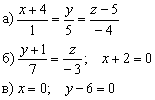
Решение: Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений снимаем точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

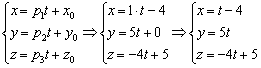
Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку , координаты которой, скажем, соответствуют значению параметра :

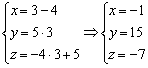
Таким образом: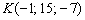

б) Рассмотрим канонические уравнения . Выбор точки здесь несложен, но коварен: (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор , а на оставшееся место поставим ноль: .

Составим параметрические уравнения прямой:

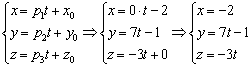
в) Перепишем уравнения в виде , то есть «зет» может быть любым. А если любым, то пусть, например, . Таким образом, точка принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули: 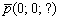. На оставшееся место ставим единицу: . Вместо единицы подойдёт любое число, кроме нуля.

Запишем параметрические уравнения прямой:

Не нашли, что искали? Воспользуйтесь поиском: