Угол между двумя прямыми. Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0

Угол φ между двумя прямыми, заданными общими уравнениями A₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0, вычисляется по формуле:

Угол φ между двумя прямыми, заданными каноническими уравнениями (x-x₁)/m₁ = (y-y₁)/n₁ и (x-x₂)/m₂ = (y-y₂)/n₂, вычисляется по формуле:

Расстояние от точки до прямой

3,2

Каждую плоскость в пространстве можно представить как линейное уравнение, называемое общим уравнением плоскости

,

Частные случаи.

o Если в уравнении (8) , то плоскость проходит через начало координат.

o При (, ) плоскость параллельна оси (оси , оси ) соответственно.

o При (, ) плоскость параллельна плоскости (плоскости , плоскости ).

· Даны точки , , . Составить уравнение плоскости .

Решение: используем (7)

,

.

Ответ: общее уравнение плоскости .

· Пример.

Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости . Запишите координаты всех нормальных векторов этой плоскости.

Решение.

Нам известно, что коэффициенты при переменных x, y и z в общем уравнении плоскости являются соответствующими координатами нормального вектора этой плоскости. Следовательно, нормальный вектор заданной плоскости имеет координаты . Множество всех нормальных векторов можно задать как .

Ответ:

· Пример.

Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку , а - нормальный вектор этой плоскости.

Решение.

Приведем два решения этой задачи.

Из условия имеем . Подставляем эти данные в общее уравнение плоскости, проходящей через точку :

· Пример.

Напишите общее уравнение плоскости параллельной координатной плоскости Oyz и проходящей через точку .

Решение.

Плоскость, которая параллельна координатной плоскости Oyz, может быть задана общим неполным уравнением плоскости вида . Так как точка принадлежит плоскости по условию, то координаты этой точки должны удовлетворять уравнению плоскости , то есть, должно быть справедливо равенство . Отсюда находим . Таким образом, искомое уравнение имеет вид .

· Требуется написать уравнение плоскости, проходящей через точку и параллельной векторам и .

Решение. Векторное произведение по определению 10.26 ортогонально векторам p и q. Следовательно, оно ортогонально искомой плоскости и вектор можно взять в качестве ее нормального вектора. Найдем координаты вектора n:

то есть . Используя формулу (11.1), получим

Раскрыв в этом уравнении скобки, приходим к окончательному ответу.

Ответ: .

· Найти единичный нормальный вектор плоскости .

Перепишем вектор нормали в виде 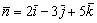и найдём его длину:

Согласно вышесказанному:

Ответ:

· Построить плоскость, проходящую через точку параллельно плоскости .

У параллельных плоскостей один и тот же вектор нормали. 1) Из уравнения найдём вектор нормали плоскости: .

2) Уравнение плоскости составим по точке и вектору нормали :

Ответ:

Векторное уравнение плоскости в пространстве

Параметрическое уравнение плоскости в пространстве

Не нашли, что искали? Воспользуйтесь поиском: