
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
Ранг матрицы – это максимальное количество линейно независимых строк.
Итак, метод Гаусса (или, иначе, метод последовательного исключения неизвестных) состоит в следующем:
1.
Путем элементарных преобразований систему уравнений приводят к эквивалентной ей системе с верхне-треугольной матрицей. Эти действия называют прямым ходом.
Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
3.
При этом все преобразования проводятся над так называемой расширенной матрицей системы, которую и приводят к верхнее - треугольному виду в прямом ходе метода.
система имеет бесчисленное множество решений, так как ранг матрицы меньше числа неизвестных.
что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
1,2
 Обратным ходом метода Гаусса найдем корни системы. Из последнего уравнения найдем корень х3: -5/2x3 = 3/2, x3 = (3/2):(-5/2) = 3/2*(-2/5) = -3/5. Корень x3 = -3/5 найден. Подставим его в верхнее (второе) уравнение системы (-2x2-3x3 = 1): -2x2-3(-3/5) = 1, -2x2+9/5 = 1, -2x2 = 1-9/5, -2x2 = -4/5, x2 = (-4/5):(-2) = (-4/5)*(-1/2) = 2/5. Корень x2 = 2/5 найден. Подставим его и корень х3 в верхнее (первое) уравнение системы (x1-x2+x3 = 0): Обратным ходом метода Гаусса найдем корни системы. Из последнего уравнения найдем корень х3: -5/2x3 = 3/2, x3 = (3/2):(-5/2) = 3/2*(-2/5) = -3/5. Корень x3 = -3/5 найден. Подставим его в верхнее (второе) уравнение системы (-2x2-3x3 = 1): -2x2-3(-3/5) = 1, -2x2+9/5 = 1, -2x2 = 1-9/5, -2x2 = -4/5, x2 = (-4/5):(-2) = (-4/5)*(-1/2) = 2/5. Корень x2 = 2/5 найден. Подставим его и корень х3 в верхнее (первое) уравнение системы (x1-x2+x3 = 0):
| x1-2/5+(-3/5) = 0, x1-5/5 = 0, x1 = 5/5 = 1. Проверка:  т. е. т. е. 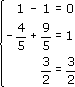 т. е. т. е.  и т. д. и т. д.
|
1,3
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Необходимость
Пусть система совместна. Тогда существуют числа  такие, что
такие, что 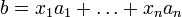 . Следовательно, столбец
. Следовательно, столбец 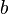 является линейной комбинацией столбцов
является линейной комбинацией столбцов  матрицы
матрицы  . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что
. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что  .
.
Достаточность
Пусть  . Возьмем в матрице
. Возьмем в матрице  какой-нибудь базисный минор. Так как
какой-нибудь базисный минор. Так как  , то он же и будет базисным минором и матрицы
, то он же и будет базисным минором и матрицы  . Тогда, согласно теореме о базисном миноре, последний столбец матрицы
. Тогда, согласно теореме о базисном миноре, последний столбец матрицы  будет линейной комбинацией базисных столбцов, то есть столбцов матрицы
будет линейной комбинацией базисных столбцов, то есть столбцов матрицы  . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы
. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы  .
.
1,4
При транспонировании квадратной матрицы её определитель не меняется: 
Общий множитель в строке можно выносить за знак определителя.
Если две строки определителя поменять местами, то определитель поменяет знак.
Определитель с двумя равными строками равен нулю.
Определитель с двумя пропорциональными строками равен нулю.
Определитель, содержащий нулевую строку, равен нулю.
Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Определитель – это некоторое число поставленное в соответствие квадратной матрице  .
.
Не нашли, что искали? Воспользуйтесь поиском: