Свойства операций над векторами.

Итак, мы определили операцию сложения векторов и операцию умножения вектора на число. При этом для любых векторов и произвольных действительных чисел можно при помощи геометрических построений обосновать следующие свойства операций над векторами. Некоторые из них очевидны.

1. Свойство коммутативности .

2. Свойство ассоциативности сложения .

3. Существует нейтральный элемент по сложению, которым является нулевой вектор , и 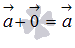. Это свойство очевидно.

4. Для любого ненулевого вектора существует противоположный вектор и верно равенство . Это свойство очевидно без иллюстрации.

5. Сочетательное свойство умножения . К примеру, растяжение вектора в 6 раз можно произвести, если сначала его растянуть вдвое и полученный вектор растянуть еще втрое. Аналогичного результата можно добиться, например, сжав вектор вдвое, а полученный вектор растянуть в 12 раз.

6. Первое распределительное свойство . Это свойство достаточно очевидно.

7. Второе распределительное свойство . Это свойство справедливо в силу подобия треугольников, изображенных ниже.

8. Нейтральным числом по умножению является единица, то есть, . При умножении вектора на единицу с ним не производится никаких геометрических преобразований.

Векторное пространство (линейное пространство) - множество элементов, называемых векторами, для которых определены операции сложения и умножения на число. Простейший, но важный пример - совокупность векторов a, b, c,... обычного 3-мерного пространства. Каждый такой вектор - направленный отрезок, задаваемый тремя числами: ; числа называются координатами вектора. При умножении вектора на вещественное число соответствующий отрезок, сохраняя направление, растягивается в раз: . Сумма двух векторов находится по правилу параллелограмма; если и то . Паре векторов a и b сопоставляют также скалярное произведение (см. Векторная алгебра). Непосредственным обобщением З-мерного пространства является n -мерное евклидово пространство. Его элементы - упорядоченные наборы вещественных чисел, Например, , 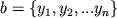. Сложение и умножение векторов на число определены формулами 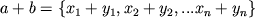, , а скалярное произведение - формулой Примером комплексного бесконечномерного векторного пространства может служить совокупность комплексных функций f, заданных на всей оси и квадратично суммируемых (то есть имеющих конечный интеграл ). Многие классы функций, например, полиномы заданного порядка, функции непрерывные, дифференцируемые, интегрируемые, аналитические и тому подобные, также образуют бесконечномерные векторные пространства.

В трёхмерном пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:

1. Длина нуль-вектора, 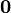, равна нулю; длина любого другого вектора положительна.

2. Умножение вектора на положительное число во столько же раз увеличивает длину вектора.

3. Действует неравенство треугольника.

Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным пространством.

2,2

Не нашли, что искали? Воспользуйтесь поиском: