
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Параметрическое уравнение плоскости
Пусть в координатном пространстве 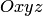 заданы:
заданы:
а) точка  ;
;
б) два неколлинеарных вектора (рис.4.15).
Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам  и проходящей через точку
и проходящей через точку 
Выберем на плоскости произвольную точку  . Обозначим
. Обозначим 
 -радиус-векторы точек
-радиус-векторы точек  и
и  (рис.4.16).
(рис.4.16).
Точка  принадлежит заданной плоскости тогда и только тогда, когда векторы
принадлежит заданной плоскости тогда и только тогда, когда векторы 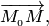
 и
и  компланарны (см. разд. 1.3.2). Запишем условие компланарности: где
компланарны (см. разд. 1.3.2). Запишем условие компланарности: где  — некоторые действительные числа (параметры). Учитывая, что
— некоторые действительные числа (параметры). Учитывая, что  получим векторное параметрическое уравнение плоскости:
получим векторное параметрическое уравнение плоскости:
| (4.19) |
где  — направляющие векторы плоскости, а
— направляющие векторы плоскости, а  — радиус-вектор точки, принадлежащей плоскости.
— радиус-вектор точки, принадлежащей плоскости.
Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:
| (4.20) |
где  и
и  — координаты направляющих векторов
— координаты направляющих векторов  и
и  соответственно. Параметры
соответственно. Параметры  в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины
в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины  пропорциональны расстоянию от заданной точки
пропорциональны расстоянию от заданной точки  до точки
до точки  принадлежащей плоскости. При
принадлежащей плоскости. При  точка
точка  совпадает с заданной точкой
совпадает с заданной точкой  . При возрастании
. При возрастании 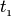 (или
(или  ) точка
) точка  перемещается в направлении вектора
перемещается в направлении вектора  (или
(или  ), а при убывании
), а при убывании 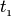 (или
(или  ) — в противоположном направлении.
) — в противоположном направлении.
Не нашли, что искали? Воспользуйтесь поиском: