Второй способ, позволяющий находить расстояние от точки до прямой a в пространстве.

Так как в условии задачи нам задана прямая a, то мы можем определить ее направляющий вектор и координаты некоторой точки М₃, лежащей на прямой a. Тогда по координатам точек и мы можем вычислить координаты вектора : (при необходимости обращайтесь к статье координаты вектора через координаты точек его начала и конца).

Отложим векторы и от точки М₃ и построим на них параллелограмм. В этом параллелограмме проведем высоту М₁H₁.

Очевидно, высота М₁H₁ построенного параллелограмма равна искомому расстоянию от точки М₁ до прямой a. Найдем .

С одной стороны площадь параллелограмма (обозначим ее S) может быть найдена черезвекторное произведение векторов и по формуле 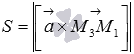. С другой стороны площадь параллелограмма равна произведению длины его стороны на высоту, то есть, , где - длина вектора , равная длине стороны рассматриваемого параллелограмма. Следовательно, расстояние от заданной точки М₁ до заданной прямой a может быть найдена из равенства как .

Итак, чтобы найти расстояние от точки до прямой a в пространстве нужно

· определить направляющий вектор прямой a () и вычислить его длину ;

· получить координаты некоторой точки М₃, лежащей на прямой a, вычислить координаты вектора , найти векторное произведение векторов и как и получить его длину ;

· вычислить требуемое расстояние от точки до прямой в пространстве по формуле .

Не нашли, что искали? Воспользуйтесь поиском: