Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве.

Рассмотрим решение примера.

Пример.

Найдите расстояние от точки до прямой .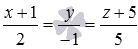

Решение.

Первый способ.

Напишем уравнение плоскости 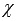, проходящей через точку М₁ перпендикулярно заданной прямой:

Найдем координаты точки H₁ - точки пересечения плоскости 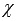и заданной прямой. Для этого выполним переход от канонических уравнений прямой к уравнениям двух пересекающихся плоскостей

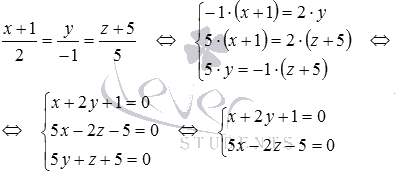
после чего решим систему линейных уравнений 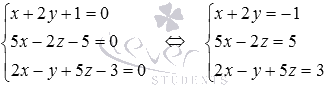методом Крамера:

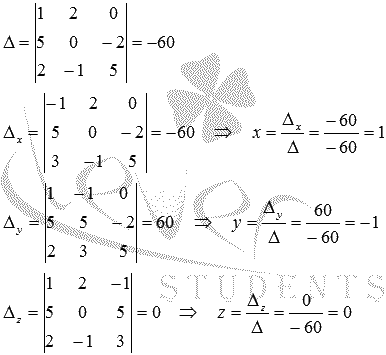
Таким образом, .

Осталось вычислить требуемое расстояние от точки до прямой как расстояние между точками и :
.

Второй способ.

Числа, стоящие в знаменателях дробей в канонических уравнениях прямой, представляют собой соответствующие координаты направляющего вектора этой прямой, то есть, 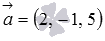- направляющий вектор прямой 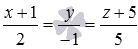. Вычислим его длину: .

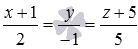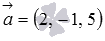Очевидно, что прямая проходит через точку , тогда вектор с началом в точке и концом в точке есть . Найдем векторное произведение векторов и :

тогда длина этого векторного произведения равна .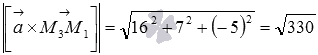

Теперь мы располагаем всеми данными, чтобы воспользоваться формулой для вычисления расстояния от заданной точки до заданной плоскости: .

Ответ:

.

Взаимное расположение прямых в пространстве

http://mathus.ru/math/ll.pdf

Не нашли, что искали? Воспользуйтесь поиском: