Проекция точки на плоскость

· Определите координаты проекции точки М1(-1,-2.5) на плоскость

x-2y+2z-4=0

Нормальный вектор плоскости x-2y+2z-4=0

имеет координаты (1.-2.2), следовательно, вектор является направляющим вектором прямой a. Теперь мы можем написать параметрические уравнения прямой в пространстве, так как знаем координаты точки прямой М1(-1,-2.5) и координаты ее направляющего вектора (1.-):

X=1t-1

Y=-2t-2

Z=2t+5

Осталось определить координаты точки пересечения прямой и плоскости. Для этого в уравнение плоскости подставим :
.

Теперь по параметрическим уравнениям вычислим значения переменных x, y и z при :
.

Таким образом, проекция точки М₁ на плоскость АВС имеет координаты .

Проекция прямой на плоскость

Эллипс

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусам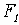и и есть величина постоянная (ее обозначают через 2*а). Причем эта постоянная больше расстояния между фокусами.

Для вывода уравнения эллипса выберем систему координат так, чтобы фокусы F₁ и F₂ лежали на оси , а начало координат совпадало с серединой отрезка F₁F₂. Тогда фокусы будут иметь следующие координаты: и .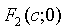

Пусть — произвольная точка эллипса. Тогда, согласно определению эллипса, , т. е.

(11.5)

Это, по сути, и есть уравнение эллипса.

Преобразуем уравнение (11.5) к более простому виду следующим образом:

,

,

,

,

.

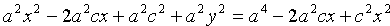Так как a > с, то 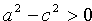. Положим

(11.6)

Тогда последнее уравнение примет вид или

(11.7)

Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Обычно обозначается “ ” или “ ”.

Форма эллипса (мера его "сжатия") характеризуется его эксцентриситетом.