Глава 10. Наука в период античного рабовладельческого общества 1 страница

Развитие письменности. Греческая и латинская письменность произошла из финикийской. Возникновение архаического греческого письма относится приблизительно к IX — VIII вв. до н. э.
В дальнейшем греческая письменность разделилась на несколько разновидностей. На основе восточно-греческого письма появилась классическая греческая (аттическая) письменность. Названия букв были заимствованы греками у финикийцев, хотя значение их было полностью утрачено: «алэп» (голова быка) стал «альфат», «гамл» (голова и шея верблюда) — «гаммой» и т. д. Некоторые знаки приобрели новое звучание. Греки ввели также ряд дополнительных букв, например «фи», «хи», унаследованных впоследствии старославянской кириллицей.
К IV в. до н. э. греки перешли к принятому позднее во всех европейских языках способу письма слева направо, в то время как финикийцы писали справа налево, что сохранилось в ряде восточных языков.
На основе западно-греческого письма в VIII—VII вв. до н. э. возникла этрусская, а затем латинская письменность. Классический латинский алфавит сложился ко II в. до н. э. Римляне не давали буквам особых названий. «Альфа» превратилась просто в «а», «бета» в «бе» и т. д.

Что касается цифровых систем, то у греков существовала вначале так называемая аттическая система, при которой имелись особые знаки для 1, 5, 10, 50 и некоторых других чисел. Знак I исходно обозначал поднятый палец, знак V—ладонь с отставленным большим пальцем (т.е. пять пальцев), знак Х — две скрещенные руки (т е. 10 пальцев). Однако впоследствии (около V в. до н.э.) утвердилась ионическая алфавитная цифровая система, где числа обозначались буквами (тысячи — с добавлением штриха), например: а (альфа) — 1, i (йота) — 10, р (ро) — 100 и т. д.
В латинской же письменности сохранился принцип аттической системы (пришедшей через этрусков): 1 обозначалось как I, 2—II, 5—V, 10—X, 50—L, 100—С и т.д.
В Индии, завоеванной Дарием I, после 522 г. до н. э. начинает распространяться цифровая символика, подобная финикийской системе цифровой записи. В Индии эта система опиралась на особые знаки для 1, 4, 10, 20, 100 и их скорописное группирование. Они использовались до III в. до н. э., затем были вытеснены цифровыми символами индийской письменности, в которой имелись специальные символы для каждого из чисел от 1 до 9. Все эти преобразования явились предпосылкой создания индийской позиционной системы
счисления.
В конце I в. до н. э. индейцы майя разработали двадцатичную
систему счисления, основанную на счете пальцев рук и ног. В ней был представлен и нуль'. Индейцы делили ее на две подсистемы. Первая включала знаки для 1, 5 и 0 и была более распространенной. Вторая содержала иероглифы от 1 до 13 и нуль и использовалась для записи только календарных вычислений. С ее помощью записывались
большие числовые величины.
В IV в. до н. э. была создана саламинская доска — древнейшие сохранившиеся счеты2, являвшиеся основным счетным прибором вплоть до эпохи Возрождения. Вычисления осуществлялись перемещением счетных костей и камешков (калькулей) на плоскостяхуглублениях для отдельных рядов десятков, что требовало вычислений в уме до 10.
Примерно с VII в. до н. э. греки писали на папирусе кистью или особой палочкой. Листок папируса по-гречески назывался «хартес» и «бйблион» или «бйблос». От первого слова происходит старославянское «хартия» и латинское charta, вошедшее в форме «карта» во все европейские языки. Слово «бйблион», означавшее не только листок папируса, но также письмо, сочинение, книгу, напоминало о заимствовании греческой письменности у финикийцев. Библ — изменен-
'Некоторые ученые датируют возникновение этой системы счисления IV в до н. э 2 У греков эта доска называлась «абак», у китайцев «суан-нан», у японцев wa-
роб-ян» и т д
'От лат. calculus — камень образовалось calculator — калькулятор, счетчик, вычислитель

Бронзовая счетная доска. I в. н. э.
ное греками название финикийского города Гебла или Гебала. Этот корень получил впоследствии самое широкое применение в слове «библиотека» и множестве терминов, относящихся к книжному делу.
О технологии изготовления писчего материала из папируса сообщил римский ученый Плиний Старший. Острой иглой стебель делили на длинные и широкие волокна. На доску укладывали рядом полоски папируса, затем клали поперечные полоски. Все это смачивали илистой водой из Нила, служившей отличным соединительным материалом. Полученный влажный лист отжимали при помощи пресса, сушили на солнце. Листы отбивали молотком, после чего папирус разглаживали. Длина свитка составляла 8—10 м. Его сворачивали, обматывая вокруг палки с загнутыми концами. В античные времена эта палка называлась «пупом» свитка — дочитать свиток до «пупа» значило дочитать его до конца.
На папирусе писали драматурги Эсхил и Аристофан, философ Сократ, математик и механик Архимед, историк Геродот.
Папирусные свитки были предметом гордости многих библиотек мира. В прославленной крупнейшей библиотеке древнего мира Александрийской, основанной в III в. до н. э., в лучшие ее времена насчитывалось до 700 тыс. свитков.
С III в. до н.э. в античном мире получает распространение в качестве материала для письма пергамент, или пергамен,— особым

образом выделанная кожа телят и козлят'. Ее название связано с именем малоазиатского городагосударства Пергама, важного центра эллинистической культуры, где выделка пергамента получила большое развитие2.
Листы пергамента первоначально сшивались так же,, как прежде соединялись листы папируса. Вошедшее во все европейские языки словом «том» греческого происхождения, оно напоминает о временах, когда рукописи оформлялись в виде свитков. «Томос» значит «отрезанная часть», т. е. часть рукописи в виде отдельного свитка. По сравнению с хрупкими папирусными листами пергамент обладал неисчислимыми преимуществами. Писали на нем с обеих сторон; смыв краску, на нем можно было писать повторно. Но главное преимущество пергамента состояло в том, что его можно было легко сгибать, не боясь сломать, как папирус.
О распространении письменности в эллинистических государствах свидетельствует не только
' Использование кожи в качестве материала для письма известно с глубокой древности (в Египте—со II тыс. до н.э.). Поскольку пергамент был очень дорог, использование более грубых сортов кожи продолжалось и после его изобретения.
Изготовление пергамента
Находки в пещерах на берегу Мертвого моря показали, что даже изолировань я Кумранская община (II в. до н. э.—I в. н. э.) располагала хранилищем в 600 рукописных свитков на коже, пергаменте и папирусе.
'По традиции возникновение пергамента связывали с именем пергамского царя Евмена И, который во II в. до н.э. задумал создать в своей столице большую библиотеку. Об этом прослышал властитель Египта Птолемей V, страстный книголюб и гордец. Боясь, что новая библиотека может затмить славу Александрийской библиотеки, он наложил запрет на вывоз папируса. Тогда Евмен и решил создать новьш материал, прозванный по имени его столицы пергаментом. Евмен все-таки создал библиотеку, где хранилось 200 тыс. свитков.

Приемы переписки книг
наличие грандиозных библиотек, но и повседневная жизнь населения античного мира Греки и римляне производили деловые и бытовые записи, а также применяли при обучении детей деревянные дощечки, покрытые с одной стороны воском,— кодициллий (codicilli — от слова codex — ствол дерева, бревно)'.
Для быстрой записи под диктовку вольноотпущенник Цицерона (106—43 гг. до н. э.) Тирон, служивший у него секретарем, изобрел римскую стенографию. Буквы процарапывались на мягком воске железным грифелем, острым с одной стороны, тупым с другой (для затирания написанного). Грифель этот назывался «стилос» или
'Отсюда происходит и слово «кодекс». Исходное значение этого выражения — деревянная книга Нынешнее значение «свод законов» это слово приобрело лишь позднее.

К оглавлению
160

«стиль». От названия этого инструмента произошло и современное слово «стиль», сначала означавшее почерк, затем литературный слог, а в дальнейшем систему выразительных приемов. Концы дощечек скрепляли между собой металлическими скобками, ремешком и просто веревкой. Получалось некоторое подобие тетради. В зависимости от количества страниц тетрадка эта называлась диптихом (две страницы), триптихом (три страницы), полиптихом (много страниц).
Когда в римских владениях пергамент получил широкое распространение, то куски кожи (примерно со II в.) также стали отрезать в виде отдельных больших листов и сшивать их в тетрадки. Корешок тетради прошивался, чтобы листы не выпадали. Затем несколько тетрадей сшивали друг с другом. Книгу, составленную из нескольких тетрадок, древние римляне называли «кодекс». Появление таких кодексов, в частности «Кодекс Синатикуса», относится к IV в. н. э.
Переплеты книг изготовлялись вначале из деревянных дощечек, обтянутых кожей, иногда по углам окованных металлом, а позднее делались с тиснеными или инкрустированными украшениями, застежками и т. д. Вот почему в русском языке до сих пор существует выражение «прочесть от доски до доски», хотя книжные переплеты давно уже делают из картона и бумаги. На пергаменте и папирусе греки и римляне писали чернилами с помощью заостренного тростника. Чернила делались из смеси сажи и гуммиарабика или чернильных орешков. Чернильницы изготовлялись из бронзы, глины и дерева.
Родиной туши является Китай (III в. до н.э.). Поскольку тушь ввозилась в страны Средиземноморья через Индию, в Римской империи она именовалась «индийскими чернилами»'.
В 102 г китайский ученый Цай Лунь (48—118 гг.) открыл способ получения бумаги из древесной коры, конопли, тряпья и т. п. Для изготовления бумаги очищенное от листьев сырье резали на тонкие куски, замачивали в извести и вываривали несколько суток. Полученную массу отцеживали, тщательно размалывали и разбавляли водой до получения клейкой кашицеобразной массы. В эту массу погружалась черпальная форма, представлявшая собой деревянную раму с сеткой из прочных шелковых ниток. Затем форма вынималась, вода стекала через сетку, и на поверхности ее оставался тонкий слой волокон. Этот слой вместе с черпальной рамой клали под пресс. Затем спрессованные листы складывали один на другой в кипу и отжимали. Бумажные листы высушивали на раскаленной каменной печи и, наконец, разрезали.
Общая характеристика развития античной науки. Наибольших успехов развитие точных и естественных наук достигло в грекоримском мире (включая эллинистический Восток), в Индии и Китае. Можно отметить некоторые общие черты научного развития во всех названных странах, несмотря на все своеобразие их культур.
Во-первых, научное познание имело еще нерасчлененный, недиф-
' Это было унаследовано английским языком По-английски тушь—Indian ink
6 Зак 2985 В С Виргинский
161

Почтовая марка, посвященная Цай Луню
ференцированный характер. Отсюда энциклопедичность знаний наиболее крупных ученых древности.
Во-вторых, при господстве целостного восприятия природы естественные науки являлись составной частью натурфилософии, а потому в них отразилась борьба между материализмом и идеализмом, которая возникла одновременно с зарождением этих направлений общественной мысли.
В-третьих, хотя в естественных науках этой эпохи учитывался накопленный практический опыт, результаты наблюдений и исследований, но наука о природе основывалась прежде всего на отвлеченных, умозрительных принципах и на авторитетах предшественников. Мы уже видели, что многие ученые были вместе с тем и изобретателями. Но обычно их деятельность в области техники осуществлялась параллельно с научно-философской.
В античный период начинается обособление науки от религии. Правда, не следует преувеличивать завершенности этого процесса. Сознание философов еще не освободилось от традиций анимистического и мифологического восприятия мира. Но все же отдельные передовые мыслители подвергли решительной критике традиционные религиозные представления. За вольнодумие афинский философ Анаксагор (V в. до н. э.) едва не поплатился жизнью, подобно Сократу. В естественных и точных науках того периода, являвшихся составной частью натурфилософии, отразилась борьба между идеалистическими и материалистическими воззрениями. Эта борьба характерна для научной мысли как средиземноморских стран, так и Индии и Китая.

Математика. К античной эпохе относится возникновение математики' как самостоятельной науки. Создание математики было вызвано практическими запросами материального производства, а также потребностями других наук.
Прежде всего следует сказать о деятельности Пифагора (ок. 570 — ок. 500 гг. до н. э.) и его школы. Собственно математические труды Пифагора представляют значительный интерес. Он открыл математическую закономерность в музыке и стал основоположником математической акустики. Ему принадлежат важные заслуги в применении математики в астрономии. Большую роль в развитии математики сыграли и последователи Пифагора — пифагорейцы. Они сформулировали десять пар противоположных категорий — бинарных оппозиций2, соединение которых, по их мнению, обусловило возникновение и поддержание порядка в мире. Знаменитая теорема Пифагора приписывается ему именно потому, что только его школа доказала справедливость ее общей формулировки.
Вместе с тем в трудах пифагорейской школы проявились и мистико-идеалистические воззрения. Умозрительные рассуждения, подчеркивание количественной стороны природных явлений привели пифагорейцев к числовой мистике. Придавая мистический характер учению о числах, они разыскивали в них особое, таинственное значение.
В V в. до н. э. Зенон Элейский (ок. 490 — ок. 430 гг. до н. э.) сформулировал ряд парадоксов — апорий, указав на связь между потенциальной и актуальной бесконечностью. Из парадоксов, которые сохранились, самой знаменитой является апория об Ахиллесе и Геракле. Парадоксы Зенона рассматривают как первую форму мыслительного эксперимента.
Огромный вклад в разработку математики внесла знаменитая ионийская школа' и продолжатели ее натурфилософских трудов (V— IV вв. до н. э.). Уже упомянутый «вольнодумный» философ Анаксагор (ок. 500—423 гг. до н. э.) впервые выдвинул идею бесконечно малой величины. Она нашла развитие и практическое применение в геометрии (определение объема шара, конуса и т.д.), в трудах Демокрита (атомистическая теория) и Евдокса Книдского (ок. 408 — ок. 355 гг. до н. э.). Последний разработал также учение о пропорциональности, чем способствовал преодолению кризиса пифагорейской математики, вызванного открытием иррациональных чисел. Постро-
Треческое слово «математика» происходит от «матэма»—значение, учение, наука Математикой иногда называли астрономию и астрологию
•'К ним относятся' «предел—бесконечное», «нечетное—четное», «одно— множество», «правое—левое», «мужское—женское», «покоящееся—движущееся», «прямое — кривое», «свет — тьма», «доброе — злое», «квадратное — продолговаточетырехугольное»
Ионией называлась часть побережья Малой Азии, где располагались высокоразвитые в экологическом и культурном отношении греческие города Холофон, Эфес, Милет и др

енная им теория, включавшая в себя как отношения целых чисел, так и отношения геометрических отрезков, представляла собой античную форму современной теории действительных чисел. Евдокс Книдский разработал метод исчерпывания (античная форма теории предела) и применял его для решения математическими средствами парадоксов Зенона. Созданный им метод исчерпывания оказал заметное влияние на развитие идей о бесконечно малых величинах.
Первую попытку систематизировать достижения -геометрии сделал хиосский математик Гиппократ (ок. 440 г. до н. э.). Древнегреческий геометр доказал, что существуют определенные плоские фигуры, ограниченные дугами окружности, для которых можно найти прямоугольники равновеликой площади (гиппократовы луночки). Открытие Гиппократа послужило началом других исследований в области квадратуры круга.
Эти и некоторые другие исследования математиков (в частности, пифагорейцев) были предшественниками работ Евклида из Александрии (ок. 340 или ок. 365. — ок. 287 или ок. 300 гг. до н. э.), автора знаменитых «Элементов». В этом своем труде, состоящем из тринадцати книг, он впервые изложил важнейшие положения геометрии (планиметрии и стереометрии) в строго продуманной логической (дедуктивной) системе. Разработанная Евклидом система аксиом и постулатов явилась для многих поколений математиков примером использований аксиоматического метода.
Ученик Евклида Аполлоний Пергский (ок. 262 — ок. 190 гг. до н. э. или 260—170 гг. до н.э.) был автором классического труда о конических сечениях. Идеи, высказанные Аполлонием, оказали большое влияние на развитие аналитической геометрии, проективной геометрии и функционального анализа.
Древнегреческий ученый-энциклопедист Эратосфен Киренский (ок. 276—194 гг. до н.э.) создал способ нахождения простых чисел («сито Эратосфена») и выдвинул идею измерения дуги медианы.
Разносторонний деятель античной науки и техники, Архимед из Сиракуз (ок. 287—212 гг. до н. э.) выдвигал в математике оригинальные и смелые идеи. Он приближался к открытию исчисления бесконечно малых величин Эвдокса. Применив античные методы вычисления, Архимед вычислил квадратуру параболы, длину спирали Архимеда, значение числа л. В своем труде «О числе песчинок» он привел алгоритм получения все больших натуральных чисел.
Развитие математики на эллинистическом Востоке, в Индии и Китае также привело к важным новым открытиям. В месопотамскую математику во времена Селевкидов (III в. до н. э.) в состав цифр был введен знак для нуля. В китайском трактате «Математика в девяти главах» (II в. до н.э.) впервые приводились отрицательные числа и правила операций над ними. В «Математике...» представлен способ решения уравнений второй и третьей степени, основанный на вычислении второй и третьей степени двучлена; решение системы п-линейных уравнений с х-неизвестными и т. д. Всего «Математика...» содержала 246 задач с указаниями к их решению.

Китайский астроном Чжан Хэн (78—139 гг.) выдвинул утверждение, что вторая степень длины окружности относится ко второй степени периметра квадрата, описанного вокруг окружности, как 5:8. С введением в III в. в Китае десятичной системы мер китайские математики начинают использовать десятичные дроби. В III — IV вв. н. э. были написаны основные части известной древнекитайской математической рукописи «Десять классических трактатов».

В соседней с Китаем стране—| Индии в это же время при решении комбинаторных задач математики использовали биноминальные коэффициенты. В IV — V вв. в Индии распространяются астрономо-математические трактаты «Сиддаханты», написанные учеными, покинувшими Александрию после Аристотель разрушения ее научного центра.
Диофант Александрийский (326—410 или II пол. III в.) опубликовал «Арифметику», сочетавшую древнегреческие традиции. В этом трактате были впервые представлены алгебраическая символика, решение неопределенных уравнений в рациональных положительных числах, составлена часть теории чисел. Тем самым были заложены основы первой буквенной алгебраической системы.
Астрономия. Астрономия медленно освобождалась от фантастических представлений, питаемых религиозными традициями и преимущественно умозрительным характером античной натурфилософии. Последнему противостоял прежде всего накопленный запас наблюдений над видимым движением небесных светил и другими астрономическими явлениями. Однако даже ионийцы выдвигали в астрономии ряд совершенно произвольных гипотез. По Фалесу Милетскому (625— 547 гг. до н. э.), Земля имеет форму плоского диска, плавающего на поверхности океана, по Анаксимандру' (ок. 610—ок. 546 гг. до н. э.) — форму цилиндра, а по Анаксимену (ок. 548—528 или 525 гг. до н. э.) — форму стола.
Лишь позже было выдвинуто предположение, что и Земля, и все светила имеют форму шара. Это утверждение принадлежит пифагорейцам. Они же отошли от мысли о том, что Земля занимает
'Анаксимандр составил также карту звездного неба, которая значительно облегчала плавание в ночное время.

центральное положение во Вселенной (геоцентризм). Один из ученых-пифагорейцев — Филолай (ок. 470 — ок. 390 гг. до н. э.) утверждал, будто шарообразная Земля, Солнце, Луна и другие планеты вращаются вокруг некоего «центрального огня», находясь
в прозрачной сфере.
Уже упоминавшийся математик Евдокс вернулся к геоцентрической идее. Он доказывал, что Земля находится в центре Вселенной, а вокруг нее вращаются прозрачные сферы, объемлющие одна другую, на которых расположены светила.
Аристотель (384—322 гг. до н. э.) попытался обобщить эмпирические космологические сведения и также создал собственную геоцентрическую систему мира с подлунной и надлунной сферами.
К гениальным натурфилософским догадкам древних относится гипотеза астронома Аристарха Самосского (310—230 гг. до н. э. или ок. 320—250 гг. до н. э.) о вращении шарообразной Земли вокруг оси и о движении ее вокруг Солнца. Он предположил также, что диаметр Солнца в 7 раз больше диаметра Земли, а расстояние от Земли до Солнца в 12 раз больше расстояния до Луны. Однако его идеи встретили противодействие <И были оставлены без внимания. Крупнейшие античные ученые позднейшего периода вернулись к геоцентрической теории.
Аполлоний Пергский, желая более точно согласовать эту теорию с астрономическими наблюдениями, выдвинул теорию эпициклов. Планеты будто бы движутся по круговым орбитам, а центры этих орбит, в свою очередь, вращаются вокруг Земли. Аполлонию приписывают изобретение астролябии — прибора для измерения
высоты звезд.
Его современник Архимед, в юности проводивший астрономические наблюдения, изготовил планетарий, приводившийся в движение
водой.
Выдающийся астроном древности Гиппарх (ок. 180(190) — 125 гг. до н. э.) примкнул к теории Аполлония и развил ее. Однако эти ошибочные мнения не помешали Гиппарху сделать несколько важнейших астрономических открытий, основанных на множестве наблюдений и на удивительно точных вычислениях. Гиппарх первым стал пользоваться понятиями широты и долготы для определения положения различных пунктов на Земле. С большой точностью определил он расстояние от Земли до Луны и до Солнца. Ему удалось рассчитать продолжительность солнечного года (с точностью до 6 минут), наклон к солнечному экватору, открыть прецессию точки весеннего равноденствия, определить параллакс Луны, эксцентриситет солнечной орбиты и т. д.
В трудах Гиппарха приводятся установившиеся к тому времени названия звезд, созвездий и планет. Большинство этих названий, сохранившихся до наших дней, имело мифологическое происхождение. В 134 г. до н. э. Гиппарх обнаружил новую звезду, вспыхнувшую в созвездии Скорпиона. Это побудило его составить звездный каталог, включавший более 1000 звезд.

Геоцентрическая система Вселенной получила наиболее полное развитие в трудах александрийского астронома, математика и географа Клавдия Птолемея (ок. 85 — ок. 160 гг.), прежде всего в его сочинении «Великое математическое построение астрономии в XIII книгах» («Syntaxis Magiste»). Основываясь на теоретических рассуждениях Аполлония Пергского об эпициклах, он по сути дела описал геоцентрическую систему Гиппарха. По Птолемею, шарообразная Земля неподвижно расположена в центре Вселенной. Вокруг нее находятся прозрачные сферы, объемлющие одна другую, вместе с которыми (в соответствии со сложными эпициклами) движутся светила. За

Клавдий Птолемей
сферой неподвижных звезд Птолемей поместил «жилище блаженных». Система Птолемея господствовала в Европе и после крушения Римской империи.
В Китае наблюдение за светилами существовало с незапамятных времен. В IV в. до н. э. уже был составлен звездный каталог, включавший около 800 объектов. К этому же времени относится древнекитайская книга «Основы определения звезд».
Во II в. н. э. выдающийся китайский астроном Чжан Хэн также сделал много важных открытий. Составленный им каталог неподвижных звезд значительно превышал каталог Гиппарха — в нем содержалось 2,5 тыс. звезд. В работе «Строение Вселенной» он указал, что Луна имеет форму шара и излучает «несобственный» свет (т. е. является только отражателем света). Чжан Хэн был не только наблюдателем, но и конструктором научных приборов. Он создал первый небесный глобус, воспроизводивший движение светил. Ему также приписывается изобретение сейсмографа оригинальной конструкции.
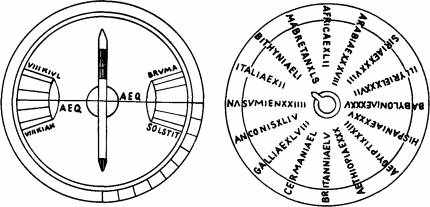
Развитие календаря. Одним из важных практических применений астрономических наблюдений было уточнение календаря. С древнейших времен греки пользовались лунным календарем, в основу которого был положен год в 354 дня, делившийся на 12 месяцев — гекатомбайон (соответствующий примерно июлю), метагейтнион, боэдромион и др. Через каждые три года на четвертый добавлялся один дополнительный месяц (2-й посейдон), чтобы не нарушать соответствия между временем года и отдельными явлениями природы.

Вместе с тем общегреческий календарь отсутствовал. Каждый полис имел собственный календарь.
В 593 г. до н. э. афинский правитель Солон по примеру вавилонян установил 8-летний период, в котором 3 года имели 13 месяцев, остальные 5 лет—12 месяцев, но этот календарь был не совсем точным и был принят не везде.
В 432 г. до н. э. греческий математик и астроном Метон установил зависимость между лунным месяцем и солнечными годами. Метон определил 19-летний цикл, включавший в себя 7 лет по 13 месяцев, остальные годы имели 12 месяцев. Этот календарь надолго установился в Афинах.
Македонский календарь отличался от афинского названиями месяцев (диос, аудинеос и др.) и тем, что он начинался не летом, а осенью (первый месяц соответствовал октябрю-ноябрю). В результате завоеваний Александра Македонского этот календарь получил распространение в Сирии, Малой Азии, Египте и т. д. Отставание лунного года от солнечного требовало периодических поправок, вносимых в летосчисление. Так, 7 марта в 238 г. до н. э. постановлением Птолемея III к 365-дневному году в каждый четвертый (високосный) год добавлялся «переходный» день.
В III в. до н. э. афинский историк Тимей ввел систему летосчисления по олимпиадам, которые проводились один раз в четыре года. Началом отсчета стал 776 г. до н. э — год проведения первых игр в Олимпии. Годы рассчитывались с полнолуния, следующего после летнего солнцестояния, и обозначались порядковым номером олимпиады и номером года в четырехлетии. Олимпийская система летосчислен-ия стала общеэллинской. Греки не знали семидневной недели, месяц делился на 3 декады Постепенно, под влиянием древнееврейского календаря, греки стали делить месяц на семидневки.
В древнейший период существования Рима использовался своеобразный лунный календарь, состоявший из 10 месяцев и включавший 304 дня. Началом летосчисления по традиции считался год основания Рима — 753 г. до н. э. Месяцы в римском календаре имели попеременно 30 и 31 день. Первым месяцем в году был март (марциус), а последним декабрь—децембер. Понятно, что месяцы передвигались во времени, соответствуя то одному, то другому периоду года.
Первую реформу календаря легенда приписывает римскому царю Нуме Помпилию и относит к VII в. до н. э. Нума, приняв во внимание разницу между лунным и солнечным годом, ввел в римский календарь два месяца — январь и февраль. В календаре Нумы семь месяцев имели по 29 дней, четыре—по 31, а февраль составлял 28 дней. Календарь состоял из 355 дней. Календарный год в целом делился на 44 восьмидневные недели и три дня. Последний день каждой недели назывался нундиной (от «новем» — девять)' — это был рыночный, праздничный день
'Последний день старой недели римляне считали первым днем новой недели, в результате чего восьмой день считался девятым

В 46 г. до н. э. по приказу Юлия Цезаря александрийские астрономы во главе с Сосигеном (Созиген) произвели реформу римского календаря'. Год стал исчисляться в 365 дней, а каждый четвертый год — 366 дней. В новом календаре сохранился только один добавочный день, помещавшийся после 23 февраля2. Таким образом, шестой день до мартовских календ стал двойным (bissextilis), от чего и прозошло наше слово «високосный». Начало года переносилось на 1 января. Юлианский год приблизился к астрономическому солнечному, но все же несколько запаздывал по сравнению с ним (за 128 лет это отставание составляло сутки). В честь Юлия Цезаря римский месяц квинтилис был переименован в юлиус. Позднее император Август велел назвать своим именем месяц секстилис. С эпохи Августа, т. е. с I в. н. э., римские месяцы имеют знакомые нам названия. Первое число месяца, совпадающее с новолунием, называлось у римлян календами3, за ними следовали ноны — 5-е или 7-е число, день первой четверти Луны, а 13 или 15 число приходилось на иды. С IV в. н.э. в римский календарь введена семидневная неделя.
К VI в. китайские астрономы установили, что новолуние совпадает с летним солнцестоянием не через 8 лет, а через каждые 19 лет, или 235 лунных месяцев. Поэтому уже в 595 г. до н. э. в Китае начал действовать лунно-солнечный календарь, включавший 19-летний цикл, в течение которого 7 лет (3, 6, 8, 11, 14, 16 и 19) имели по 13 месяцев. Примерно в III в. до н. э. у сельского населения Китая сложился свой хозяйственный год, который делился на 24 сезона. Одновременно счет проводили по 60-летним циклам с началом летосчисления в 2397 г. до н. э. Каждый год цикла носил название какого-либо животного, а каждые два года посвящались одной из пяти стихий (дерево, огонь, земля, железо, вода).
Похожий календарь существовал и у древних евреев с IV в. до н. э.
В Индии существовали как лунно-солнечные, так и солнечные календари с годом в 360 или 365 дней, добавлявшиеся через каждые пять лет. Месяцы имели от 29 до 32 дней. В Индии одновременно существовало около 20 календарей (эр) преимущественно религиозного характера.
У древних майя существовали и лунные, и солнечные календари. Все они возникли в первые века нашей эры. По солнечному календарю 365—366-дневный год включал 18 месяцев, в каждом из которых было по 20 дней. В конце года добавлялось 5 дней. Неделя имела 13 дней. Месяцы лунного календаря имели 29 и 30 дней.
'Эта реформа представляет для нас особый интерес, поскольку юлианский календарь через Византию был принят на Руси и существовал в нашей стране до Октябрьской революции 1917 г
'По традиции после 23 февраля 191 г до н э жрецы-понтифики имели ежегодно право вводить дополнительный месяц — мерцедоний, равный 23 или 22 дням
'Отсюда произошло крылатое выражение «до греческих календ», т е никогда Ведь в греческом календаре календ не было

Не нашли, что искали? Воспользуйтесь поиском: