Оптимизация геометрии трещины в газоконденсатных пластах

Вполне вероятно, в газоконденсатных пластах что на работу трещины будет оказывать сильное отрицательное влияние наличие жидкого конденсата, что равносильно повреждению поверхности трещины. Чтобы оценить этот эффект, примем, что пластовое давление на границе этой «поврежденной» зоны должно быть точно равно давлению конденсации («точки росы»).

Для любой длины трещины и данного динамического забойного давления, находящегося внутри зоны ретроградной конденсации двухфазной огибающей, профиль давления по нормали к фазе трещины и внутрь пласта будет оконтуривать точки, где давление равно давлению конденсации. Из этого профиля давления можно определить распределение скина поверхности трещины. Глубина пораженной зоны определяется из уравнения 5-16, модифицированного выражения Синко-Лея и Саманиего. Дополнительный необходимый элемент — это ухудшение относительной проницаемости, задаваемое корреляционной зависимостью, представленной в уравнениях 5-10 — 5-14.

Ниже приводится исследование этого явления на двух примерах фактических данных. В первом примере принимаем пласт с проницаемостью 5 мД и давлением конденсации 2545 psi (17.55 МПа). Динамическое забойное давление равно 1800 psi (12.41 МПа). Сначала стандартная оптимизация трещины ГРП — игнорируя эффекты скина на поверхности трещины — с использованием числа проппанта, , равного 0.02, дает ожидаемую безразмерную проводимость трещины 1.6 и полудлину трещины 220 футов (67 м) для квадратного пласта со стороной 4000 футов (1219 м). (Это значение числа проппанта, если принять = 50000 мД, = 50 футов (15.2 м), 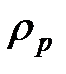= 165 фунт/куб.фут (2643 кг/м³) и f_p = 0.4, дает массу проппанта приблизительно в 80 000 фунтов (36 287 кг)). Безразмерный индекс продуктивности будет равен 0.35.

Серия модельных расчетов, основанных на работе Ванга и др., показывает максимальный индекс продуктивности, который может быть достигнут при введении газоконденсатного скина, а также указывает на соответствующие изменения в дизайне трещины. Длина трещины прогрессивно увеличивается, тогда как число проппанта (т.е., масса нагнетенного проппанта) остается постоянной. Это, конечно, вызывает неизбежное уменьшение проводимости трещины, даже при максимизации индекса продуктивности.

Результаты, приведенные на рис. 5-6, показывают оптимальную полудлину трещины в 225 футов (77.7 м) (16-процентное увеличение от оптимума для нулевого скина) и оптимальную безразмерную проводимость трещины в 1.2 вместо 1.6. Намного более значительным является уменьшение оптимального индекса продуктивности до 0.294.

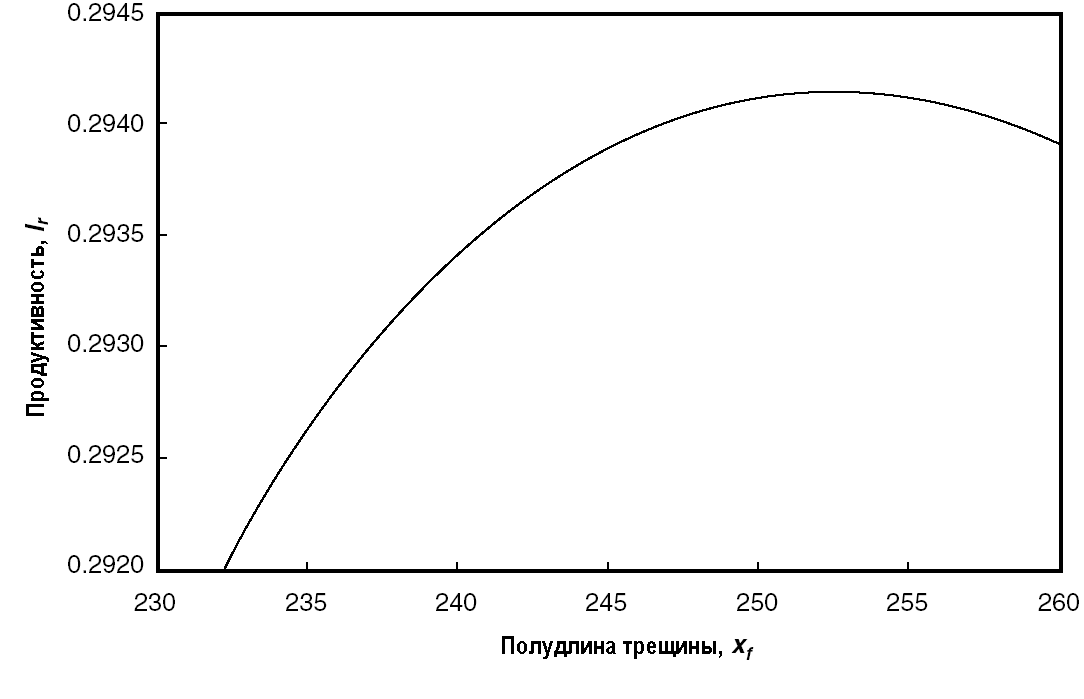
РИС. 5-6. Оптимизированная геометрия трещины в газоконденсатном пласте (k = 5 мД).

Чтобы получить ожидаемый индекс продуктивности 0.35 для нулевого скина, потребовалось бы увеличить число проппанта приблизительно до 0.045 — и более чем удвоить требуемую массу проппанта.

Для пласта с намного большей проницаемостью (200 мД) — снова, игнорируя вначале скин поверхности трещины — те же расчеты дают оптимальную полудлину трещины, равную 35 футов (10.7 м) (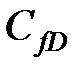 = 1.6). Число проппанта для этого случая равно 0.0005 (для той же массы проппанта 80000 фунтов = 36 287 кг). Соответствующий безразмерный индекс продуктивности равен 0.21.

На рис. 5-7 приведена оптимизация размеров трещины с газоконденсатным повреждением, показывающая, что оптимальная полудлина трещины равна 45 футов (13.7 м) (увеличение на 30 процентов относительно оптимума для нулевого скина). Новый оптимальный 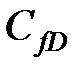равен 1, а соответствующий индекс продуктивности равен 0.171.

Здесь отрицательное влияние газоконденсатного повреждения на индекс продуктивности, а также меры противодействия этому намного более серьезные. Требуемое число проппанта становится 0.003 — те есть в 6 раз больше проппанта, чем предполагалось изначально! В большинстве случаев такой гидроразрыв был бы весьма нереальным, так что приходится значительно урезать радужные ожидания относительно эффективности скважины.

РИС. 5-7. Оптимизированная геометрия трещины в газоконденсатном пласте (k = 200 мД).

Не нашли, что искали? Воспользуйтесь поиском: