Определения и допущения

Дебит газа рассчитывается из уравнения для продуктивности в псевдостационарном режиме:

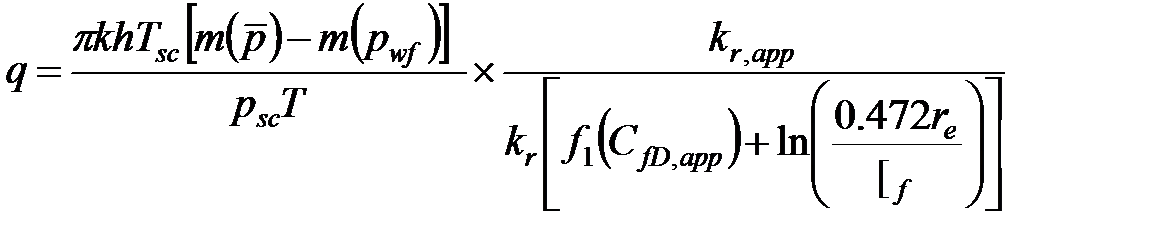(5-17)

где 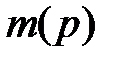есть функция псевдодавления, — 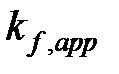— кажущаяся проницаемость проппанта в трещине, и — кажущаяся проницаемость пласта. (Все уравнения в этом подразделе даны в согласованной системе единиц, такой как СИ.) Функция 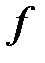была введена Синко-Леем и Саманиего [Cinco-Ley and Samaniego, 1981], она была представлена в главе 3 как

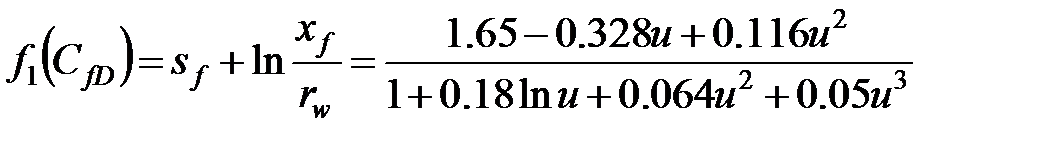(5-18)

где .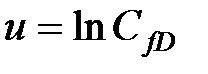

Кажущаяся безразмерная проводимость трещины определяется выражением

(5-19)

Кажущиеся проницаемости зависят от скорости потока; следовательно, уравнение для продуктивности становится неявно зависящим от дебита.

Чтобы двигаться дальше, нам требуется некоторая модель течения не по закону Дарси. Для этого почти исключительно используется уравнение Форчхеймера:

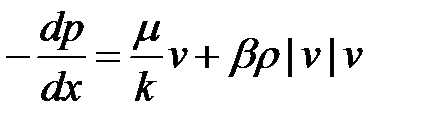(5-20)

где 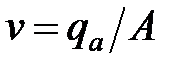есть скорость Дарси, а b — свойство пористой среды.

Популярная корреляционная зависимость была представлена Фирузабади и Кацем [Firoozabadi and Katz, 1979] в виде

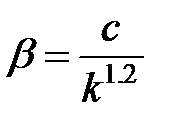(5-21)

где c = 8.4 × 10^–8 м^1.4 (= 2.6 × 10¹⁰ фут^–1 мД^1.2).

Чтобы применить корреляционную зависимость Фирузабади и Каца, запишем

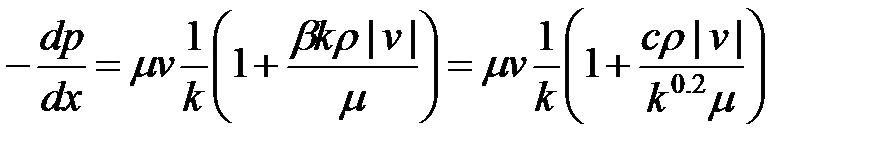(5-22)

что показывает, что

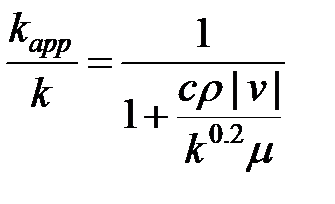(5-23)

Приведенное выше уравнение можно использовать как для пласта, так и для трещины, если подставить правильную представительную линейную скорость. В последующих выкладках принимаем, что .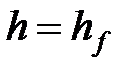

Представительная линейная скорость для пласта может быть выражена через дебит газа как

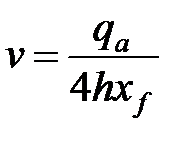(5-24)

где — объемный дебит ин ситу (фактический); следовательно, для эффекта отклонения от закона Дарси в пласте имеем

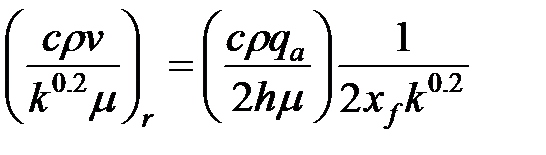(5-25)

Представительная линейная скорость в трещине может быть выражена через дебит газа как

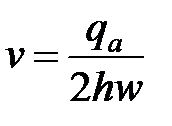(5-26)

Таким образом, для эффекта отклонения от закона Дарси в трещине можно использовать выражение

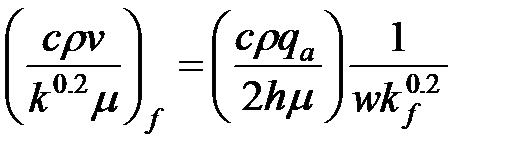(5-27)

Член 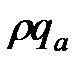есть массовый дебит, и он одинаковый в пласте и в трещине; crq_a выражается через дебит газа как

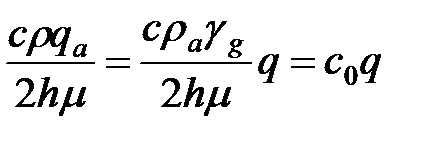(5-28)

где 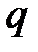есть дебит газа в стандартном объеме за единицу времени, 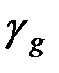— удельный вес газа относительно воздуха, а 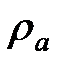— плотность воздуха при стандартных условиях. Множитель 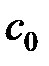постоянный для данной системы пласт-трещина.

Конечный вид зависимости кажущейся проницаемости от дебита следующий

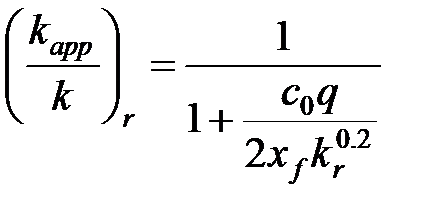(5-29)

для пласта и

(5-30)

для трещины. Как следствие, уравнение для продуктивности приобретает вид

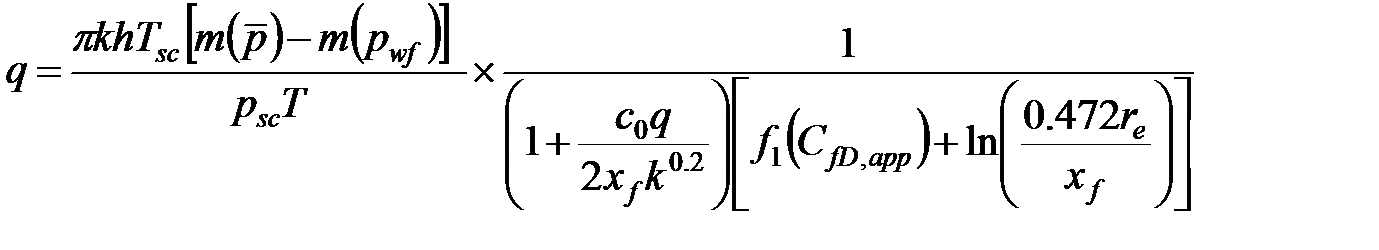(5-31)

где

(5-32)

Дополнительный скин-эффект, 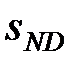, появляющийся из-за течения не по закону Дарси, может быть выражен как

(5-33)

Дополнительный скин-эффект за счет течения не по закону Дарси всегда положительный и зависит от дебита нелинейно.

Уравнения 5-31 и 5-33 чрезвычайно важны для интерпретации данных испытаний после гидроразрыва и для прогноза добычи. Если не понимать ясно механизм, отвечающий за скин-эффект после гидроразрыва, можно допустить грубые ошибки в оценке обработки пласта и в прогнозе добычи.

Не нашли, что искали? Воспользуйтесь поиском: