
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения задач 1 страница
Глава III. ЭЛЕКТРИЧЕСТВО
1. Электрическое поле создаётся тонкой бесконечно длинной нитью, равномерно заряженной с линейной плотностью заряда t = 1×10-10 Кл/м. Определить поток вектора напряжённости N через цилиндрическую поверхность длиной l = 2 м, ось которой совпадает с нитью.
| Дано: t = 1×10-10 Кл/м l = 2 м | Решение. Заряды могут быть распространены в пространстве либо дискретно, либо непрерывно. Для характеристики непрерывного распределения электрических зарядов вдоль неко- |
| N ‑? |
торой линии, по некоторой поверхности или по некоторому объёму вводится понятие о плотности зарядов. Если электрические заряды непрерывно распределены вдоль линии, то вводится линейная плотность зарядов t:
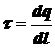 ,
,
где dq – заряд малого участка линии длиной dl.
По условию данной задачи бесконечно длинная нить заряжена с одинаковой линейной плотностью заряда t, значит, электрические заряды непрерывно распределены вдоль этой нити. Следовательно, заряд малого участка dl данной нити равен
 .
.
Рассмотрим данную нить.
Согласно принципу суперпозиции напряжённость электростатического поля, создаваемого непрерывно распределёнными вдоль нити зарядами, равна
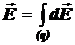 ,
,
где 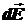 ‑ напряжённость электростатического поля, создаваемого малым зарядом dq, а интегрирование проводится по всем непрерывно распределённым вдоль первой нити зарядам. Малый заряд dq можно считать точечным электрическим зарядом. Следовательно,
‑ напряжённость электростатического поля, создаваемого малым зарядом dq, а интегрирование проводится по всем непрерывно распределённым вдоль первой нити зарядам. Малый заряд dq можно считать точечным электрическим зарядом. Следовательно,
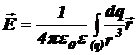 ,
,
где  ‑ радиус-вектор, проведённый из места нахождения заряда dq в рассматриваемую точку поля,
‑ радиус-вектор, проведённый из места нахождения заряда dq в рассматриваемую точку поля,
e0 = 8,85×10-12 Ф/м – электрическая постоянная,
e – относительная диэлектрическая проницаемость среды; для вакуума e = 1.
Поток напряжённости электрического поля N сквозь поверхность S равен алгебраической сумме потоков сквозь все малые участки этой поверхности:
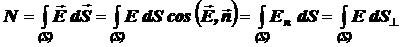 ,
,
где 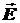 ‑ вектор напряжённости электрического поля в точках площадки dS,
‑ вектор напряжённости электрического поля в точках площадки dS,
 ‑ единичный вектор, нормальный к площадке dS,
‑ единичный вектор, нормальный к площадке dS,
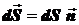 ‑ вектор площадки,
‑ вектор площадки,
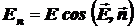 ‑ проекция вектора
‑ проекция вектора 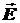 на направление вектора
на направление вектора  ,
,
 ‑ площадь проекции элемента dS поверхности на плоскость, перпендикулярную вектору
‑ площадь проекции элемента dS поверхности на плоскость, перпендикулярную вектору 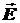 .
.
При этом все векторы  нормалей к площадкам dS должны быть направлены в одну и ту же сторону относительно поверхности S. Например, в случае замкнутой поверхности S (см. рис.) все векторы
нормалей к площадкам dS должны быть направлены в одну и ту же сторону относительно поверхности S. Например, в случае замкнутой поверхности S (см. рис.) все векторы  нормалей должны быть либо внешними, либо внутренними.
нормалей должны быть либо внешними, либо внутренними.

Так как по условию задачи необходимо определить поток вектора напряжённости N в вакууме через замкнутую поверхность, то воспользуемся теоремой Остроградского – Гаусса: поток напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность, проведённую в поле, пропорционален алгебраической сумме qохв. электрических зарядов, охватываемых поверхностью:
 ,
,
где все векторы 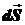 направлены вдоль внешних нормалей к замкнутой поверхности интегрирования S, которую часто называют гауссовой поверхностью.
направлены вдоль внешних нормалей к замкнутой поверхности интегрирования S, которую часто называют гауссовой поверхностью.
Поскольку длина цилиндрической поверхности равна l, то алгебраическая сумма qохв. электрических зарядов, охватываемых данной поверхностью, равна
 .
.
Таким образом, поток вектора напряжённости N через цилиндрическую поверхность длиной l, ось которой совпадает с нитью, равен
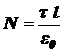 .
.
 .
.
Ответ:  .
.
2. В вершинах квадрата со стороной a = 4 см расположены точечные заряды q = 4,4 нКл. Определить работу перемещения заряда q0 = 2,2 нКл из центра квадрата в середину одной из его сторон.
| Дано: a = 4 см = 4×10-2м q = 4,4 нКл = 4,4×10-9Кл q0 = 2,2 нКл = 2,2×10-9Кл | Решение. Пусть заряда q0 перемещается из центра квадрата O в точку C (середину одной из сторон данного квадрата) в электрическом поле, созданном точечными зарядами, расположенными в вершинах квад- |
| A ‑? |
рата. Тогда работа по перемещению заряда q0 в электрическом поле
A = q0 (jO - jC),
где jO – потенциал поля в точке O,
jC – потенциал поля в точке C.
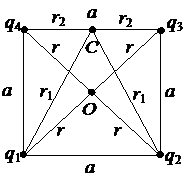
Потенциал в центре квадрата O равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:
jO = j1 + j2 + j3 + j4,
где j1, j2, j3, j4 – потенциалы, создаваемые 1 -м, 2 -м, 3 -м, 4 -м зарядами (см. рис.) соответственно в точке O.
Поскольку потенциал поля в точке, удалённой на расстояние r от точечного электрического заряда q, равен
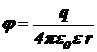 ,
,
а все данные четыре заряда равноудалены от точки O на расстояние
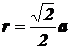 ,
,
то
 .
.
Здесь e0 = 8,85×10-12 Ф/м – электрическая постоянная,
e – относительная диэлектрическая проницаемость среды; для вакуума e = 1.
Следовательно,
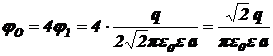 .
.
Аналогично потенциал в середине C одной из сторон данного квадрата равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:
jC = j1/ + j2/ + j3/ + j4/,
где j1/, j2/, j3/, j4/ – потенциалы, создаваемые 1 -м, 2 -м, 3 -м, 4 -м зарядами (см. рис.) соответственно в точке C.
Потенциалы поля, создаваемого 1 -м и 2 -м зарядами в точке C, удалённой на расстояние
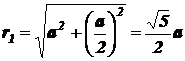
от точечных электрических зарядов q1 и q2, равны
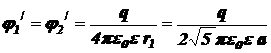 .
.
Потенциалы поля, создаваемого 3 -м и 4 -м зарядами в точке C, удалённой на расстояние
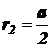
от точечных электрических зарядов q3 и q4, равны
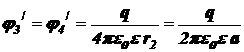 .
.
Следовательно,
 .
.
Значит,
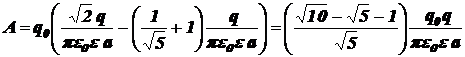 .
.
 .
.
Ответ: 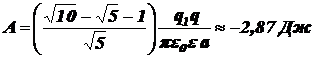 .
.
3. Сколько тепла выделится в спирали с сопротивлением R = 75 Ом при прохождении через неё количества электричества q = 100 Кл, если ток в спирали равномерно убывает до нуля в течение Dt = 50 с.
| Дано: R = 75 Ом q = 100 Кл Iк = 0 Dt = 50 с | Решение. При прохождении электрического тока по проводникам они нагреваются. Согласно закону Джоуля – Ленца количество теплоты d Q, выделяющейся в проводнике за малое время dt, пропорционально квадрату силы тока I, электрическому сопротивлению R проводника и промежутку времени dt: |
| Q‑? |
 ,
,
где U = I R – напряжение на проводнике.
Силой тока, или просто током, называется скалярная величина, равная отношению заряда dq, переносимого сквозь рассматриваемую поверхность за малый промежуток времени, к величине dt этого промежутка:
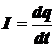 .
.
Подставляя это равенство в 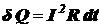 , получим
, получим
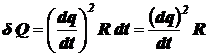 .
.
Переходя от бесконечно малого промежутка времени dt к конечному интервалу Dt и от бесконечно малого заряда dq к конечному Dq, получим выражения:
а) для силы тока
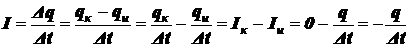 ,
,
откуда
 ,
,
где 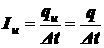 ‑ начальное значение силы тока в спирали,
‑ начальное значение силы тока в спирали,
 ‑ конечное значение силы тока в спирали;
‑ конечное значение силы тока в спирали;
б) для количества теплоты Q (перешли от d Q к Q), выделяющейся в проводнике (спирали) за время Dt,
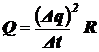 .
.
Так как  (см. выше), то
(см. выше), то
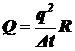 .
.
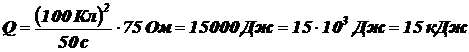 .
.
Ответ: 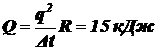 .
.
4. Между точками A и B цепи поддерживают напряжение U = 20 В. Найти ток и его направление в участке CD, если R = 5 Ом.
| Дано: U = 20 В R1 = R4 = R = 5 Ом R2 = R3 = 2R | Решение. Пусть токи, которые текут через резисторы 1, 2, 3, 4, равны I1, I2, I3, I4 соответственно, ток через перемычку CD равен I и ток, исходящий из A и приходящий в B, равен I0. Из обобщённого закона Ома для произвольного |
| I ‑? |
участка цепи
I0RAB = U
определим ток I0:
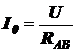 ,
,
где RAB – сопротивление между точками A и B,
U ‑ напряжение между точками A и B цепи.
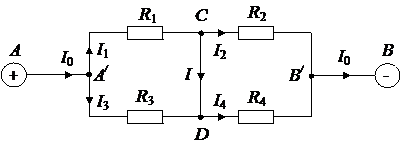
Резисторы 1 и 3 соединены параллельно, а общее сопротивление R параллельно соединённых проводников связано с сопротивлениями Ri этих проводников соотношением
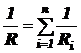 ,
,
где n – количество параллельно соединённых проводников.
Значит, общее сопротивление RACD участка цепи ACD находим из соотношения
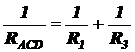 ,
,
где R1 и R3 – сопротивления резисторов 1 и 3 соответственно.
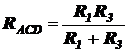 .
.
По условию задачи R1 = R, R3 = 2R.
Следовательно,
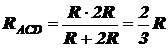 .
.
Аналогично резисторы 2 и 4 соединены параллельно.
Значит, общее сопротивление RCDB участка цепи CDB
 ,
,
где R2 и R4 – сопротивления резисторов 2 и 4 соответственно.
По условию задачи R2 = 2R, R4 = R.
Следовательно,
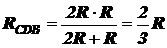 .
.
Участки ACD и CDB соединены последовательно, а общее сопротивление R цепи, состоящей из n последовательно соединённых участков, равно сумме сопротивлений Ri этих участков:
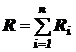 .
.
Значит, сопротивление RAB между точками A и B равно
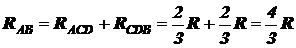 .
.
Таким образом, ток, исходящий из A и приходящий в B:
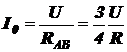 .
.
Поскольку резисторы 1 и 3 соединены параллельно, то напряжение на одном из них равно напряжению на другом:
U1 = U3.
Значит, применяя к последнему равенству обобщённый закон Ома для участка цепи, содержащего резистор 1, и участка цепи, содержащего резистор 3, получим
I1R1 = I3R3.
По условию задачи R1 = R, R3 = 2R.
Следовательно,
I1R = I3×2 R,
I1 = 2I3.
Аналогично, поскольку резисторы 2 и 4 соединены параллельно, то
I2R2 = I4R4.
По условию задачи R2 = 2R, R4 = R.
Следовательно,
I2×2R = I4 R,
2I2 = I4.
Произведём расчёт сложных (разветвлённых) цепей. Расчёт сложных (разветвлённых) цепей состоит в отыскании токов в различных участках таких цепей.
По первому правилу Кирхгофа (правилу узлов): алгебраическая сумма токов, сходящихся в узле, равна нулю:
 ,
,
где n – число проводников, сходящихся в узле,
Ii – ток в узле.
Положительными считаются токи, подходящие к узлу, отрицательными – токи, отходящие от узла.
Узлом называется точка разветвлённой цепи, в которой сходится более двух проводников.
Следовательно,
‑ для узла A/ имеем
I0 – I1 – I3 = 0.
Подставляя сюда вышенайденные I1 = 2I3 и 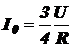 , получим
, получим
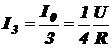 ,
, 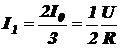 ;
;
‑ для узла B/ имеем
I2 + I4 – I0 = 0.
Подставляя сюда вышенайденные I4 = 2I2 и 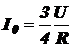 , получим
, получим
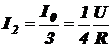 ,
, 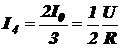 ;
;
‑ для узла C имеем
I1 – I – I2 = 0
(считаем, что ток I направлен от узла C к узлу D).
Подставляя сюда вышенайденные 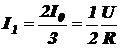 и
и 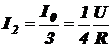 , получим
, получим
 ; (*)
; (*)
‑ для узла D имеем
I + I3 – I4 = 0.
Подставляя сюда вышенайденные 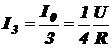 и
и 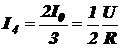 , получим
, получим
 ,
,
что совпадает с результатом, полученным ранее (см. (*)).
Таким образом, ток через перемычку CD равен
 .
.
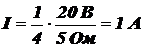 .
.
Поскольку рассчитанное значение силы тока через перемычку CD положительно, то наше предположение, что ток I направлен от узла C к узлу D, является верным. Следовательно, на участке CD ток I направлен от узла C к узлу D.
Ответ: 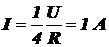 , на участке CD ток I направлен от узла C к узлу D.
, на участке CD ток I направлен от узла C к узлу D.
5. Результирующая напряжённость поля двух точечных зарядов +6,25×10-8 Кл и –10-8 Кл на расстоянии 2 см за вторым из них (на линии, проходящей через заряды) равна 0. Определить расстояние между зарядами.
Дано:
q1 = +6,25×10-8 Кл
q2 = –10-8 Кл
l = 2 см = 2×10-2 м

| Решение. Заряды могут быть распространены в пространстве либо дискретно, либо непрерывно. В данном случае заряды распространены дискретно. Согласно принципу суперпозиции (принцип суперпозиции электрических полей (принцип независимости действия электрических полей): |
| r12 ‑? |
напряжённость электрического поля системы зарядов равна геометрической сумме напряжённостей полей каждого из зарядов в отдельности), напряжённость электростатического поля, создаваемого дискретно распространёнными зарядами, равна
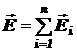 ,
,
где 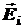 ‑ напряжённость в рассматриваемой точке пространства поля одного i -го заряда системы, а n – общее число дискретных зарядов, которые входят в состав системы.
‑ напряжённость в рассматриваемой точке пространства поля одного i -го заряда системы, а n – общее число дискретных зарядов, которые входят в состав системы.
Следовательно, напряжённость электростатического поля системы неподвижных точечных зарядов q1 и q2:
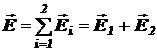 .
.
Электростатикой называется раздел учения об электричестве, в котором изучаются взаимодействия и свойства систем электрических зарядов, неподвижных относительно выбранной инерциальной системы отсчёта. (Система отсчёта, по отношению к которой материальная точка, свободная от внешних воздействий, покоится или движется прямолинейно и равномерно, называется инерциальной системой отсчёта.)
Существуют два рода электрических зарядов – положительные и отрицательные. Силы взаимодействия неподвижных тел или частиц, обусловленные электрическими зарядами этих тел или частиц, называются электростатическими силами. Разноимённо заряженные тела притягиваются, а одноимённо заряженные отталкиваются друг от друга. Точечным электрическим зарядом называется заряженное тело, форма и размеры которого несущественны в данной задаче. Например, рассматривая электрическое взаимодействие двух тел, их можно считать точечными электрическими зарядами, если размеры этих тел малы по сравнению с расстоянием между ними.
Силы электростатического взаимодействия заряженных тел подчиняются экспериментально установленному закону Кулона. Поэтому их часто называют кулоновскими силами. (Закон Кулона: сила электростатического взаимодействия двух точечных электрических зарядов прямо пропорциональна произведению этих зарядов, обратно пропорциональна квадрату расстояния между зарядами и направлена вдоль соединяющей их прямой).
Кулоновское взаимодействие между неподвижными электрически заряженными частицами или телами осуществляется посредством их электростатического поля. Электростатическое поле представляет собой стационарное (не изменяющееся с течением времени) электрическое поле.
Напряжённость электростатического поля точечного заряда qi равна
 ,
,
где  ‑ радиус-вектор, проведённый из точечного заряда qi в рассматриваемую точку поля,
‑ радиус-вектор, проведённый из точечного заряда qi в рассматриваемую точку поля,
e0 = 8,85×10-12 Ф/м – электрическая постоянная,
e – относительная диэлектрическая проницаемость среды; для вакуума e = 1.
Во всех точках поля векторы 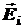 направлены от заряда qi, если qi > 0, и направлены к нему, если qi < 0.
направлены от заряда qi, если qi > 0, и направлены к нему, если qi < 0.
Направим ось x от зарядов к точке M (так, как показано на рисунке). Тогда проекция Ex вектора 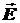 на ось x равна
на ось x равна
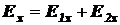 .
.
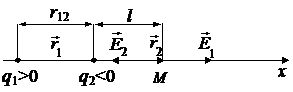
Так как q1 > 0, то вектор  направлен в рассматриваемой точке поля M в сторону от заряда по линии, проходящей через заряды q1 и q2 (точка M также находится на линии, проходящей через эти заряды (справа от обоих зарядов)), т.е. по направлению оси x.
направлен в рассматриваемой точке поля M в сторону от заряда по линии, проходящей через заряды q1 и q2 (точка M также находится на линии, проходящей через эти заряды (справа от обоих зарядов)), т.е. по направлению оси x.
Так как q2 < 0, то вектор 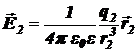 направлен в рассматриваемой точке поля M к заряду по линии, проходящей через заряды q1 и q2, т.е. в сторону, противоположную направлению оси x.
направлен в рассматриваемой точке поля M к заряду по линии, проходящей через заряды q1 и q2, т.е. в сторону, противоположную направлению оси x.
Проекция 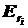 вектора
вектора 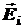 на направление радиус-вектора
на направление радиус-вектора  равна
равна
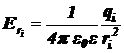 .
.
Следовательно, проекция 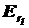 вектора
вектора 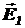 на направление радиус-вектора
на направление радиус-вектора  равна
равна
Не нашли, что искали? Воспользуйтесь поиском: