
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Примеры решения задач 2 страница
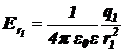 ;
;
проекция 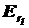 вектора
вектора  на направление радиус-вектора
на направление радиус-вектора 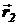 равна
равна
 .
.
Поскольку радиус-векторы  и
и 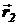 , соединяющие заряды q1 и q2 соответственно с точкой M, где вычисляется напряжённость поля, сонаправлены (
, соединяющие заряды q1 и q2 соответственно с точкой M, где вычисляется напряжённость поля, сонаправлены ( направлен от точечного заряда q1 к рассматриваемой точке поля M и
направлен от точечного заряда q1 к рассматриваемой точке поля M и 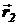 направлен от точечного заряда q2 к рассматриваемой точке поля M), а также их направления совпадают с направлением оси x, то
направлен от точечного заряда q2 к рассматриваемой точке поля M), а также их направления совпадают с направлением оси x, то
 ,
,  .
.
Значит,
 .
.
По условию задачи  , откуда
, откуда  .
.
Следовательно,
 ,
,
 .
.
Из рисунка видно, что
r1 = r12 + l, r2 = l.
Значит,
 ,
,
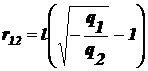 .
.
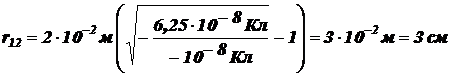 .
.
Ответ:  .
.
6. На расстоянии 5 см от поверхности металлического шара R = 2 см с поверхностной плотностью заряда 4 мкКл/м2 находится точечный заряд 1 нКл. Определить работу электрических сил при перемещении этого заряда на расстояние 8 см от поверхности шара.
| Дано: l1 = 5 см = 5×10-2м R = 2 см = 2×10-2м s = 4 мкКл/м2 = 4×10-6Кл/м2 q0 = 1 нКл = 10-9Кл l2 = 8 см = 8×10-2м | Решение. Заряды могут быть распространены в пространстве либо дискретно, либо непрерывно. Для характеристики непрерывного распределения электрических зарядов вдоль некоторой линии, по некоторой поверхности или по некоторому объёму вводится понятие о плотности за- |
| A ‑? |
рядов. Если электрические заряды непрерывно распределены по некоторой поверхности, то вводится поверхностная плотность зарядов s:
 ,
,
где dq – заряд, расположенный на малом участке поверхности площадью dS.
По условию данной задачи металлический шар заряжен с одинаковой поверхностной плотностью заряд s, значит, электрические заряды непрерывно распределены по поверхности шара. Следовательно, заряд малого участка поверхности площадью dS данного шара равен
 ,
,
откуда
 ,
,
где  ‑ площадь поверхности шара, т.е. площадь сферы.
‑ площадь поверхности шара, т.е. площадь сферы.
Следовательно,
 .
.
Работа, совершаемая силами электростатического поля при перемещении заряда q0 из точки 1 в точку 2, равна
A = q0 (j1 - j2),
где j1 – потенциал поля в точке 1,
j2 – потенциал поля в точке 2.
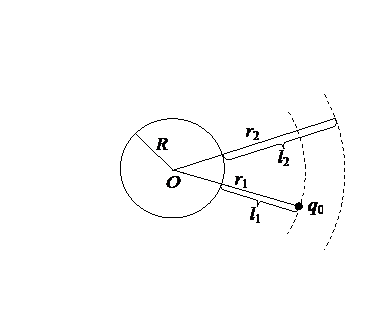
Рассмотрим электростатическое поле заряда q, равномерно распределённого в вакууме по поверхности металлического шара радиуса R с поверхностной плотностью заряда s.  (см. выше).
(см. выше).
Система зарядов и, следовательно, её поле центрально симметричны относительно центра O шара. Поэтому расчёт поля удобно провести, воспользовавшись теоремой Остроградского – Гаусса: поток напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность, проведённую в поле, пропорционален алгебраической сумме qохв. электрических зарядов, охватываемых поверхностью:
 ,
,
где e0 = 8,85×10-12 Ф/м – электрическая постоянная,
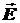 ‑ вектор напряжённости электрического поля в точках площадки dS,
‑ вектор напряжённости электрического поля в точках площадки dS,
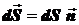 ‑ вектор площадки,
‑ вектор площадки,
 ‑ единичный вектор, нормальный к площадке dS,
‑ единичный вектор, нормальный к площадке dS,
а все векторы 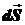 направлены вдоль внешних нормалей к замкнутой поверхности интегрирования S, которую часто называют гауссовой поверхностью.
направлены вдоль внешних нормалей к замкнутой поверхности интегрирования S, которую часто называют гауссовой поверхностью.
Для нахождения напряжённости поля 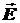 на расстоянии r от точки O следует взять за гауссову поверхность S сферу радиуса r с центром в точке O. Тогда
на расстоянии r от точки O следует взять за гауссову поверхность S сферу радиуса r с центром в точке O. Тогда
 ,
,
где Er – проекция вектора 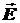 на радиус-вектор
на радиус-вектор  , проведённый из точки O в рассматриваемую точку поля.
, проведённый из точки O в рассматриваемую точку поля.
Следовательно,
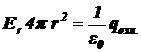 ,
,
откуда
 .
.
Если r ³ R, то qохв. = q и
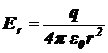 .
.
Если r < R, то qохв. = 0 и
Er = 0
(внутри сферы поля нет).
Из связи между потенциалом и напряжённостью поля (напряжённость электрического поля равна по модулю и противоположна по направлению градиенту потенциала:  ) следует, что проекция вектора напряжённости электростатического поля на произвольное направление численно равна быстроте убывания потенциала поля на единицу длины в этом направлении:
) следует, что проекция вектора напряжённости электростатического поля на произвольное направление численно равна быстроте убывания потенциала поля на единицу длины в этом направлении:  . Откуда
. Откуда
 ,
,
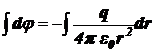 ,
,
 .
.
При изучении электростатических полей нужно знать разность потенциалов в каких-либо точках поля, а не абсолютные значения потенциалов в этих точках. Поэтому выбор точки с нулевым потенциалом определяется только удобством решения данной задачи. В связи с этим в данной задаче удобно положить j = 0 при r ® ¥. Тогда получим
0 = 0 + C,
откуда
C = 0.
Следовательно, потенциал поля вне сферы (r ³ R)
 .
.
Если заряды распределены в пространстве непрерывно (а в данной задаче электрические заряды непрерывно распределены по поверхности шара), то потенциал j их поля в вакууме (при вышеуказанном выборе точки, где j = 0) равен
 ,
,
где интегрирование проводится по всем зарядам, образующим рассматриваемую систему.
Поскольку q – заряд, распределённый по всей поверхности шара радиуса R, то при r < R
 .
.
Подставляя в это равенство  , получим
, получим
 .
.
Таким образом, внутри сферы (r < R) потенциал всюду одинаков и равен
 .
.
Из всего вышесказанного можно сделать вывод: потенциал поля в точке 1, т.е. на расстоянии r1 = R + l1 от центра шара, равен
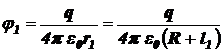 ;
;
потенциал поля в точке 2, т.е. на расстоянии r2 = R + l2 от центра шара, равен
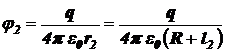 .
.
Следовательно, работа, совершаемая силами электростатического поля при перемещении заряда q0 из точки 1 в точку 2, равна
 .
.
Так как  , то
, то
 .
.
 Ответ:
Ответ:  .
.
7. В медных шинах площадью сечения 25 см2 течёт ток 250 А. Определить количество теплоты, выделяющейся в объёме 10 см3 шины за 1 мин. Удельное сопротивление меди rCu = 1,7×10-8Ом×м.
| Дано: S = 25 см2 = 25×10-4 м2 I = 250 А V = 10 см3 = 10-5 м3 Dt = 1 мин = 60 с rCu = 1,7×10-8Ом×м | Решение. При прохождении электрического тока по проводникам они нагреваются. Согласно закону Джоуля – Ленца количество теплоты d Q, выделяющейся в проводнике за малое время dt, пропорционально квадрату силы тока I, электрическому сопротивлению R проводника и промежутку времени dt: |
| Q‑? |
 ,
,
где U = I R – напряжение на проводнике.
Силой тока, или просто током, называется скалярная величина, равная отношению заряда dq, переносимого сквозь рассматриваемую поверхность за малый промежуток времени, к величине dt этого промежутка:
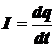 .
.
Сопротивлением R участка цепи между сечениями 1 и 2 называется интеграл
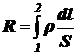 ,
,
где r ‑ удельное электрическое сопротивление среды (в данном случае медной шины, т.е. r = rCu),
dl – длина малого участка проводника (в данном случае медной шины),
S – площадь поперечного сечения проводника.
Для однородного проводника постоянного сечения (что и представляет собой в данной задаче медная шина) r = const, S = const и
 ,
,
где l12 – длина проводника между сечениями 1 и 2.
Поскольку медная шина представляет собой цилиндр, а объём цилиндра равен
V = S l,
где S – площадь поперечного сечения цилиндра,
l – образующая цилиндра, равная в данном случае рассматриваемой длине проводника между сечениями 1 и 2, т.е. l12,
то, выражая отсюда l и подставляя её в уравнение для сопротивления участка проводника  , получим
, получим
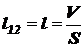 ;
;
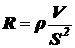 .
.
Таким образом, количество теплоты d Q, выделяющейся в проводнике за малое время dt, равно
 .
.
Переходя от бесконечно малого промежутка времени dt к конечному интервалу Dt и от d Q к Q, а также учитывая, что r = rCu, получим
 .
.
 .
.
Ответ:  .
.
8. Два элемента с e1 = 2 В и e2 = 1 В и проводник сопротивлением R = 0,5 Ом соединены по схеме, изображённой на рисунке. Внутренние сопротивления элементов одинаковы и равны r = 1 Ом каждое. Определить силу тока на всех участках цепи и разность потенциалов между точками a и b.
| Дано: e1 = 2 В e2 = 1 В R = 0,5 Ом r1 = r2 = r = 1 Ом | Решение. Пусть токи, которые текут через элемент e1, элемент e2 и проводник R, равны I1, I2, и I3 соответственно. Обобщённый закон Ома для произвольного участка цепи (рассмотрим участок AB) имеет вид: I3RAB = UAB = (jA ‑ jB) + eAB, где RAB – сопротивление между точками A и B, равное в данном случае сопротивлению проводника R; UAB ‑ напряжение между точками A и B цепи; |
| I1 ‑? I2 ‑? I3 ‑? ja ‑ jb ‑? |
(jA ‑ jB) – разность потенциалов на концах участка AB;
eAB – ЭДС всех источников электрической энергии, включенных на участке цепи AB.
Поскольку на участке цепи AB источников электрической энергии нет, то
eAB = 0.
Следовательно,
I3R = UAB = (jA ‑ jB).
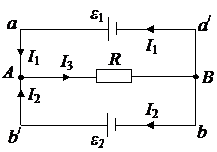
Рис. 1
(Если замкнутая цепь состоит из источника электрической энергии с ЭДС e и внутренним сопротивлением rвнутр., а сопротивление внешней части цепи равно Rвнешн., то закон Ома имеет вид
 .)
.)
Правило знаков для ЭДС источников электрической энергии, включенных на участке 1 – 2: если внутри источника ток идёт от катода к аноду, т.е. напряжённость поля сторонних сил в источнике совпадает по направлению с током на участке цепи, то при подсчёте e12 ЭДС этого источника считается положительной (см. рис. 2). Если ток внутри источника идёт от анода к катоду, то ЭДС этого источника считается отрицательной.
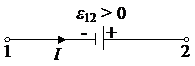

Рис. 2
Поскольку по условию задачи и e1 > 0, и e2 > 0, то ток идёт от катода к аноду. Значит, направление токов такое, как показано на рисунке 1.
Элемент e1, элемент e2 и проводник R соединены параллельно. Значит, разность потенциалов на клеммах источника e1 равна разности потенциалов на клеммах источника e2 и равна разности потенциалов на концах участка AB:
j a’ ‑ j a = j b ‑ j b’ = jA ‑ jB.
Но поскольку разность потенциалов на клеммах источника равна напряжению на внешней части цепи, т.е.
j a’ ‑ j a = e1 – I1r1, j b ‑ j b’ = e2 – I2r2,
а jA ‑ jB = I3R, то
e1 – I1r1 = e2 – I2r2 = I3R.
Откуда
 ,
,  .
.
Произведём расчёт сложных (разветвлённых) цепей. Расчёт сложных (разветвлённых) цепей состоит в отыскании токов в различных участках таких цепей.
По первому правилу Кирхгофа (правилу узлов): алгебраическая сумма токов, сходящихся в узле, равна нулю:
 ,
,
где n – число проводников, сходящихся в узле,
Ii – ток в узле.
Положительными считаются токи, подходящие к узлу, отрицательными – токи, отходящие от узла.
Узлом называется точка разветвлённой цепи, в которой сходится более двух проводников.
Следовательно, для узла A имеем
I1 + I2 – I3 = 0.
Подставляя сюда вышенайденные  и
и  , получим
, получим
 ,
,
 .
.
 .
.
Ток через элемент e2:
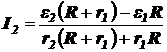 .
.
 .
.
Ток через проводник R:
 .
.
 .
.
Сопротивлением соединительных проводов пренебрегаем. Разность потенциалов между точками a и b равна разности потенциалов между точками A и B:
ja ‑ jb = jA ‑ jB.
Но jA ‑ jB = I3R (см. выше). Значит,
 .
.
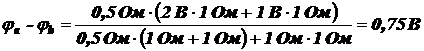 .
.
Ответ: 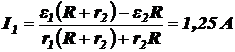 ,
,  ,
,
 ,
,  .
.
9. Заряды q1 = q2 = q3 = 1×10-6 Кл расположены в вершинах равностороннего треугольника со стороной 20 см. Найти силу, действующую на один из этих зарядов со стороны двух других, в воздухе. k = 9×109 Н×м2/Кл2.
| Дано: q1 = q2 = q3 = 1×10-6 Кл l = 20 см = 2×10-1 м k = 9×109 Н×м2/Кл2 | Решение. Электростатикой называется раздел учения об электричестве, в котором изучаются взаимодействия и свойства систем электрических зарядов, неподвижных относительно выбранной инерциальной системы |
| F ‑? |
отсчёта. (Система отсчёта, по отношению к которой материальная точка, свободная от внешних воздействий, покоится или движется прямолинейно и равномерно, называется инерциальной системой отсчёта.)
Существуют два рода электрических зарядов – положительные и отрицательные. Силы взаимодействия неподвижных тел или частиц, обусловленные электрическими зарядами этих тел или частиц, называются электростатическими силами. Разноимённо заряженные тела притягиваются, а одноимённо заряженные отталкиваются друг от друга. Точечным электрическим зарядом называется заряженное тело, форма и размеры которого несущественны в данной задаче. Например, рассматривая электрическое взаимодействие двух тел, их можно считать точечными электрическими зарядами, если размеры этих тел малы по сравнению с расстоянием между ними.
Силы электростатического взаимодействия заряженных тел подчиняются экспериментально установленному закону Кулона. Поэтому их часто называют кулоновскими силами.
Кулоновское взаимодействие между неподвижными электрически заряженными частицами или телами осуществляется посредством их электростатического поля. Электростатическое поле представляет собой стационарное (не изменяющееся с течением времени) электрическое поле.
Закон Кулона: сила электростатического взаимодействия двух точечных электрических зарядов прямо пропорциональна произведению этих зарядов, обратно пропорциональна квадрату расстояния между зарядами и направлена вдоль соединяющей их прямой.
Следовательно, сила электростатического взаимодействия двух точечных электрических зарядов q1 и q2
 ,
,
q1 и q3
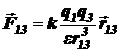 ,
,
q2 и q3
 ,
,
где e – относительная диэлектрическая проницаемость среды;
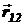 ‑ радиус-вектор, соединяющий заряд q2 с зарядом q1;
‑ радиус-вектор, соединяющий заряд q2 с зарядом q1;
 ‑ радиус-вектор, соединяющий заряд q3 с зарядом q1;
‑ радиус-вектор, соединяющий заряд q3 с зарядом q1;
 ‑ радиус-вектор, соединяющий заряд q3 с зарядом q2.
‑ радиус-вектор, соединяющий заряд q3 с зарядом q2.

Поскольку заряды q1 = q2 = q3 и расположены в вершинах равностороннего треугольника, то силы, действующие на каждый из этих зарядов со стороны двух других, одинаковые. Значит, не важно, на какой из зарядов искать силу взаимодействия со стороны двух других. В таком случае, будем искать силу взаимодействия, например, на первый заряд со стороны второго и третьего.
Суммарная сила, действующая со стороны второго заряда q2 и третьего заряда q3 на первый заряд q1, равна
 .
.
По условию задачи необходимо узнать силу, действующую на один из зарядов со стороны двух других, в воздухе. А относительная диэлектрическая проницаемость воздуха e»1. Значит,
 .
.
Так как r12 = r13 = l, q1 = q2 = q3, то
 .
.
Заряды q1, q2, и q3 расположены в вершинах равностороннего треугольника. Значит, угол между векторами 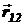 и
и  равен 600 (
равен 600 ( ).
).
Следовательно, по теореме косинусов (см. рис.)
 .
.
Так как
 ,
,
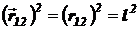 ,
,
Не нашли, что искали? Воспользуйтесь поиском: