Примеры решения задач 4 страница

Ответ: или , где R – численное значение выраженного в единицах СИ – в Ом ‑ сопротивления проводника.

17.Электрон движется в однородном магнитном поле с индукцией B = 10 мТл по винтовой линии, радиус которой R = 1,5 см и шаг h = 10 см. Определить период T обращения электрона и абсолютное значение его скорости.

Дано: B = 10 мТл = 10-2 Тл R = 1,5 см = 1,5 × 10-2 м h = 10 см = 10-1 м	Решение. Движение электрона по винтовой линии можно представить как движение по окружности со скоростью под действием силы Лоренца в плоскости, перпендикулярной индукции поля , и равномерное движение вдоль поля со скоростью (см. рис.).
T ‑ ? ‑ ?

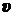Тогда полная скорость электрона

.

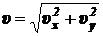Найдём отдельно скорости и .

Запишем для электрона второй закон Ньютона в проекции на ось y:

F = ma_y,

где F = eB , a_y = /R.

Тогда eBu_y = m /R, откуда = eBR/m.

Скорость u_x найдём из соотношения h = T, откуда

= h/T,

где T – период ‑ время, в течение которого электрон продвинется по горизонтальному направлению на один шаг винта h. С другой стороны, T равно времени, в течение которого электрон пройдёт со скоростью расстояние, равное длине окружности l = 2pR, т.е. T = 2pR/ ,

или с учётом того, что = eBR/m,

T = 2pm/eB.

T = 2 × 3,14× 9,11 × 10^-31 кг / (1,6 × 10^-19 Кл × 10^-2 Тл) » 35,8× 10^-10 с.

Подставив выражения = h/T = heB/2pm и = eBR/m в ,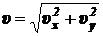

получим

.

» 38,4× 10⁶ м/с.

Ответ: T = 2pm/eB» 35,8× 10^-10 с;

» 38,4× 10⁶ м/с.

18.Заряженная частица прошла ускоряющую разность потенциалов U и влетела в скрещенные под прямым углом электрическое (E = 400 В/м) и магнитное поля (B = 0,2 Тл). Определить разность потенциалов U, если двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории. Отношение заряда к массе частицы q/m = 9.64 × 10⁷ Кл/кг.

Дано: E = 400 В/м B = 0,2 Тл 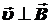q/m = 9.64 × 107 Кл/кг	Решение. На заряженную частицу в электрическом и магнитном полях действуют силы Fэл. = qE, Fмагн. = quB = quB соответственно. Поскольку заряженная частица движется прямолинейно и равномерно, электрическая и магнитная силы взаимно уравновешены.
U ‑ ?

Запишем условие равновесия заряженной частицы в проекции на ось y:

F_эл. - F_магн. = 0,

или, учитывая выражения F_эл. = qE, F_магн. = quB,

qE - quB = 0,

откуда .

Так как заряженная частица прошла ускоряющую разность потенциалов U, то работа, совершённая полем, при перемещении заряда из положения, где его скорость была равна нулю, в точку, где она стала равной , есть

A = qU.

Но так как она пошла, как уже было сказано, на изменение кинетической энергии заряженной частицы, т.е.

A = DE_к,

где DE_к = , то

qU = .

Откуда U = .

U .

Ответ: U = .

19.По двум длинным прямым параллельным проводам, расстояние между которыми d = 10 см, текут токи одинаковой силы I = 30 А. Определить магнитную индукцию B в точке, удалённой от каждого провода на расстояние r = d. Направления токов совпадают.

Дано: d = 10 см = 0,1 м I1 = I2 = I = 30 А r = d	Решение. Вектор магнитной индукции поля в точке А равен векторной сумме индукций и 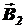полей, создаваемых в этой точке каждым током в отдельности (см. рис.):
B ‑ ?

.

Направления векторов и 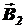определяем по правилу буравчика. Числовое значение индукции магнитного поля в точке А может быть найдено по теореме косинусов:

,

где . Следовательно,

.

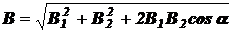Индукции магнитных полей, создаваемых каждым током в точке А, соответственно равны

, .

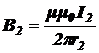Так как r₁ = r₂ = r = d, I₁ = I₂ = I, то B₁ = B₂.

Значит,

.

Так как вектор в данной точке поля А является касательной к линиям магнитной индукции, представляющим собой окружность с радиусом DA, а вектор 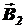в точке А является касательной к линиям магнитной индукции, представляющим собой окружность с радиусом CA, то ^ DA, 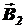^ CA. Значит, Ð DAC = .

Из D DAC по теореме косинусов найдём

.

А так как DC = d, DA = r₁ = r = d, CA = r₂ = r = d, Ð DAC = a, то

,

откуда

.

Подставив и в , получим

.

.

Ответ: .

20.Магнитная индукция B в центре кругового проводника радиуса R = 0,1 м составляет 12,6 мкТл. Определить магнитный момент p_m этого проводника с током.

Так как контур с током в данном случае представляет собой круговой виток радиуса R, то

S = pR².

Индукция магнитного поля в центре кругового витка радиуса R:

,

откуда .

Значит,

.

.

Ответ: .

21.Источник тока замкнули на катушку сопротивлением R = 2 Ом и индуктивностью L = 0,02 Гн. Через сколько времени сила тока в цепи достигнет 50% максимального значения?

Дано: R = 2 Ом L = 0,02 Гн I = 0,5 Imax	Решение. По закону Ома для замкнутой цепи , где ‑ полная ЭДС в цепи, равная в данном случае сумме ЭДС источника и ЭДС самоиндукции , возникающей после
t ‑ ?

присоединения катушки к источнику. Следовательно,

,

где ‑ ЭДС самоиндукции.

Поскольку 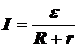, то сила тока в цепи достигает максимального значения, т.е. I = I_max,когда максимальна. А из формулы следует, что максимальна, когда минимально, или максимально (ЭДС источника тока постоянна). Min = max = 0 (I_{конечн.} > I_{начальн.}). Значит, . Откуда следует, что .

Из , учитывая, что , находим

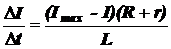
Так как скорость изменения силы тока постоянна, то , откуда , или с учётом выражения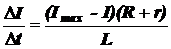

.

Пренебрегая внутренним сопротивлением источника тока r и учитывая, что по условию задачи I = 0,5 I_max, получим

.

.

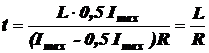Ответ: .

22.Диаметр тороида (по средней линии) D = 50 см. Тороид содержит N = 2000 витков и имеет площадь сечения S = 20 см². Вычислить энергию W магнитного поля тороида при силе тока I = 5 А. Сердечник отсутствует. Поле во всём объёме тороида считать однородным.

Дано: D = 50 см = 0,5 м N = 2000 S = 20 см2 = 2×10-3м2 I = 5 А	Решение. Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение. Тороидом называется кольцевая катушка с током, витки которой намотаны на сердечник, имеющий форму тора (см. рис.)
W ‑ ?

Если витки расположены вплотную или очень близко друг к другу, то тороид можно приближённо рассматривать как систему большого числа последовательно соединённых круговых витков одинакового радиуса, центры которых лежат на средней линии тороида, а плоскости ортогональны к ней. Из соображений симметрии следует, что линии магнитной индукции поля тороида имеют вид концентрических окружностей, центры которых лежат на оси тороида. Линиями магнитной индукции (силовыми линиями магнитного поля) называются линии, проведённые в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора магнитной индукции в этой точке поля. Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не возвращаясь вторично в любую точку поверхности.

Энергия магнитного поля соленоида (магнитное поле можно считать однородным и локализованным внутри объёма V соленоида)

,

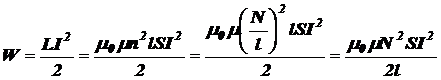где L = m₀ m n² l S – индуктивность соленоида;

‑ число витков, отнесённое к длине соленоида;

N – полное число витков в соленоиде;

l – длина соленоида;

S – площадь поперечного сечения соленоида;

m ‑ магнитная проницаемость среды, заполняющей соленоид;

m₀ – магнитная постоянная.

Итак, по формуле можно найти энергию магнитного поля соленоида. Для того, чтобы понять, можно ли её применять для нахождения энергии магнитного поля тороида, посмотрим, чем тороид отличается от соленоида.

Что собой представляет тороид, написано в начале решения задачи. Соленоидом же называется цилиндрическая катушка с током, состоящая из большого числа витков проволоки, которые образуют винтовую линию. Если витки расположены вплотную или очень близко друг к другу, то соленоид можно рассматривать как систему последовательно соединённых круговых токов одинакового радиуса с общей осью. Вектор магнитной индукции в произвольной точке, лежащей на оси соленоида, направлен вдоль этой оси.

Таким образом, тороид – это, в некотором приближении, соленоид, «изогнутый в тор». Следовательно, формула вычисления энергии магнитного поля соленоида будет справедлива и для вычисления энергии магнитного поля тороида.

Поскольку магнитная постоянная m₀ = 12,57×10^-7Гн/м, магнитная проницаемость среды, заполняющей тороид, m = 1 (воздух), длина средней линии тороида l = pD = 3,14×0,5 м = 1,57 м, полное число витков в тороиде N = 2000, площадь поперечного сечения тороида S = 2×10^-3м², сила тока I = 5 А, то

,

.

Ответ: .

23.Электрон, разогнавшись электрическим полем U = 220 В, влетает в магнитное поле B = 5×10^-3 Тл под углом 90⁰ к линиям индукции и описывает окружность R = 1 см. Найти массу электрона.

Дано: U = 220 В B = 5×10-3 Тл 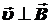R = 1 см = 10-2 м	Решение. (Движение электрона по окружности представляет собой движение со скоростью u под действием силы Лоренца в плоскости, перпендикулярной индукции поля.) На заряженную частицу в магнитном поле действует сила Лоренца
m ‑ ?

F = quB .

По условию задачи 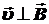, значит,

и, следовательно,

F = quB.

Запишем для заряженной частицы второй закон Ньютона в проекции на ось y:

F = ma,

где

(a_ц – центростремительное ускорение). Тогда

,

откуда

.

Так как заряженная частица прошла ускоряющую разность потенциалов U, то работа, совершённая полем, при перемещении заряда из положения, где его скорость была равна нулю, в точку, где она стала равной , есть

A = qU.

Поскольку эта работа пошла на изменение кинетической энергии заряженной частицы, т.е.

A = DE_к,

где DE_к = , то

qU = .

Подставив в это уравнение вышенайденное выражение для скорости заряженной частицы, получим

.

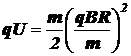Откуда

.

Заряженной частицей по условию данной задачи является электрон, поэтому

q = e.

Следовательно,

.

.

Ответ: .

24.Неподвижная проволочная квадратная рамка расположена в однородном магнитном поле, линии индукции которого перпендикулярны к плоскости рамки. По рамке скользит без нарушения электрического контакта проволочная перемычка PP^/ со скоростью ( ). В тот момент, когда перемычка пересекает центр квадрата, по ней течёт ток силой I. Определить величину и направление индукции магнитного поля. Рамка и перемычка выполнены из одного куска проволоки с удельным электрическим сопротивлением r и площадью поперечного сечения S_пров..

Дано: I r Sпров.	Решение. Для графического изображения стационарного, т.е. не изменяющегося со временем, магнитного поля пользуются методом линий магнитной индукции. Линиями магнитной индукции (силовыми линиями магнитного поля) называются линии, проведённые в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора магнитной
‑ ?

индукции в этой точке поля. Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не возвращаясь вторично в любую точку поверхности. Последний случай осуществляется, например, в магнитном поле, создаваемом системой из кругового тока и бесконечного прямолинейного проводника с током, проходящего через центр кругового витка с током, перпендикулярно к его плоскости.

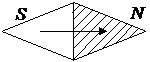
Что же касается направления вектора , то за направление вектора магнитной индукции принимается направление от южного полюса S к северному N свободно устанавливающейся в магнитном поле стрелки. Это направление совпадает с направлением положительной нормали к замкнутому контуру с током.

Положительная нормаль направлена в ту сторону, куда перемещается буравчик (с правой нарезкой), если вращать его по направлению тока в рамке.

В магнитном поле прямолинейного проводника с током магнитная стрелка устанавливается по касательной к окружности, плоскость которой (окружности) перпендикулярна проводу, а центр её лежит на оси провода. Направление вектора магнитной индукции устанавливают с помощью правила буравчика. Правило буравчика состоит в следующем: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращение ручки буравчика совпадает с направлением вектора магнитной индукции.

Магнитное поле прямоугольного контура с током I представляет собой суперпозицию магнитных полей тока в каждой из четырёх сторон этого контура. Во всех точках, лежащих в плоскости контура вектор магнитной индукции направлен перпендикулярно к этой плоскости, причём если точка находится внутри области, ограниченной контуром, то из конца вектора ток в контуре виден идущим против часовой стрелки. В точках плоскости, лежащих за пределами вышеуказанной области, вектор направлен в противоположную сторону.

Таким образом, рассматривая контур, представляющий собой квадратную рамку (OABC), по которой скользит без нарушения электрического контакта проволочная перемычка PP^/, на основании вышеизложенного можно сказать следующее. Так как при движении перемычка PP^/ делит рамку на два контура, а в тот момент, когда перемычка пересекает центр квадрата E, по ней течёт ток силой I, то в левой относительно PP^/ части контура, т.е. в контуре OACO, вектор магнитной индукции направлен перпендикулярно к этому контуру (или к рамке) вверх (перпендикулярно к чертежу на нас), поскольку в этом случае ток в левом контуре (т.е. в контуре OACO) из конца вектора виден идущим против часовой стрелки. В правой же относительно PP^/ части контура (т.е. в контуре ABCA) наоборот ‑ вектор магнитной индукции направлен перпендикулярно к этому контуру вниз (перпендикулярно к чертежу от нас). Это можно объяснить следующим образом. Все точки правой области (т.е. области ABCA) лежат за пределами вышерассмотренной левой области (т.е. области OACO). Значит, вектор в правой области противоположно направлен вектору в левой области. А поскольку в левой области вектор магнитной индукции направлен перпендикулярно к контуру вверх (перпендикулярно к чертежу на нас), то в правой области вектор магнитной индукции направлен перпендикулярно к контуру вниз (перпендикулярно к чертежу от нас). Или же: из конца вектора магнитной индукции ток должен быть виден идущим против часовой стрелки. А он виден так (идущим против часовой стрелки), если направлен (по условию задачи перпендикулярно к контуру) вниз (перпендикулярно к чертежу от нас). Значит, в правой относительно перемычки PP^/ части контура, т.е. в контуре ABCA, вектор магнитной индукции направлен перпендикулярно к контуру (или к рамке) вниз (перпендикулярно к чертежу от нас).

Не нашли, что искали? Воспользуйтесь поиском: