ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Примеры решения задач 3 страница

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

то

Отсюда

Ответ: .

10. Электрический чайник имеет две обмотки. При включении одной из них вода в чайнике закипает через 15 минут. При включении другой – через 30 минут. Через сколько минут закипит вода в чайнике, если включить обе обмотки последовательно?

Дано: t₁ = 15 минут = 900 с t₂ = 30 минут = 1800 с	Решение. При прохождении электрического тока по проводникам они нагреваются. Согласно закону Джоуля – Ленца количество теплоты d Q, выделяющейся в
t₃ ‑?

проводнике за малое время dt, пропорционально квадрату силы тока I, электрическому сопротивлению R проводника и промежутку времени dt:

где U = I R – напряжение на проводнике.

(Теплота не является видом энергии, и поэтому нельзя говорить о «запасе теплоты» в теле. По этой же причине элементарное количество теплоты d Q не является полным дифференциалом.)

Силой тока, или просто током, называется скалярная величина, равная отношению заряда dq, переносимого сквозь рассматриваемую поверхность за малый промежуток времени, к величине dt этого промежутка:

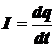Переходя от бесконечно малого промежутка времени dt к конечному интервалу Dt и от d Q к Q, получим выражение для количества теплоты Q, выделяющейся в проводнике (обмотке) за время Dt = t:

Для того, чтобы вскипятить чайник, необходимо, чтобы выделилось количество теплоты, равное Q. Если включить первую обмотку, то

откуда

где U – напряжение сети,

R₁ – сопротивление первой обмотки,

t₁ – время, за которое чайник вскипает при включении первой обмотки.

Аналогично, если включить вторую обмотку, то

откуда

где R₂ – сопротивление второй обмотки,

t₂ – время, за которое чайник вскипает при включении второй обмотки.

Так как общее сопротивление R цепи, состоящей из n последовательно соединённых участков, равно сумме сопротивлений R_i этих участков:

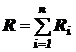то при включении обеих обмоток последовательно общее сопротивление

R_общ_. = R₁ + R₂.

Следовательно, если включить обе обмотки последовательно, то

где t₃ – время, за которое чайник вскипает при включении первой и второй обмоток последовательно.

Подставляя в это равенство сопротивления первой и второй обмоток, получим

откуда

t₃ = t₁ + t₂.

t₃ = 900 с + 1800 с = 2700 с = 45 минут.

Ответ: t₃ = t₁ + t₂ = 45 минут.

11. На каждом метре равномерно заряженной нити распределён заряд 2×10^-7 Кл. Около нити находится пылинка с зарядом – 1,65×10^-16 Кл, которая притягивается нитью с силой 10^-10 Н. На каком расстоянии от нити находится пылинка?

Дано: t = 2×10^-7 Кл/м q₀ = – 1,65×10^-16 Кл F = 10^-10 Н	Решение. Заряды могут быть распространены в пространстве либо дискретно, либо непрерывно. Для характеристики непрерывного распределения электрических зарядов вдоль некоторой линии, по некоторой поверхности или
r₀ ‑?

по некоторому объёму вводится понятие о плотности зарядов. Если электрические заряды непрерывно распределены вдоль линии, то вводится линейная плотность зарядов t:

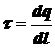где dq – заряд малого участка линии длиной dl.

По условию данной задачи нить заряжена равномерно, значит, электрические заряды непрерывно распределены вдоль этой нити. Следовательно,

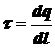откуда заряд малого участка dl нити равен

Рассмотрим нить.

Согласно принципу суперпозиции напряжённость электростатического поля, создаваемого непрерывно распределёнными вдоль нити зарядами, равна

где 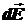‑ напряжённость электростатического поля, создаваемого малым зарядом dq, а интегрирование проводится по всем непрерывно распределённым вдоль нити зарядам. Малый заряд dq можно считать точечным электрическим зарядом. Следовательно,

,

где ‑ радиус-вектор, проведённый из места нахождения заряда dq в рассматриваемую точку поля (т.е. в условиях нашей задачи в точку нахождения пылинки).

Рассмотрим теперь взаимодействие нити и пылинки.

В электростатическом поле нити, т.е. системы точечных зарядов dq, на пылинку, т.е. на точечный заряд q₀, действует сила

.

Поскольку , то

,

где интегрирование теперь уже проводится по длине нити.

Расстояние между точечным зарядом dq первой нити и рассматриваемой точкой поля, т.е. точечным зарядом q₀ (пылинкой), можно найти по теореме Пифагора:

,

откуда

.

По правилу параллелограмма суммарный вектор сил, действующих со стороны каждого точечного заряда dq нити на точечный заряд q₀ (пылинку), перпендикулярен этой нити.

Значит, сила, действующая со стороны нити на пылинку (или сила, действующая на пылинку в электростатическом поле нити), направлена перпендикулярно данной нити. Проецируя на перпендикулярное нити направление (т.е. на ось x на рисунке), получим

,

где и поэтому перед интегралом стоит коэффициент 2. Поскольку , где , ‑ это сила, действующая со стороны одной половины нити (верхней на рисунке) на пылинку, а аналогично точно такая же сила действует со стороны другой половины нити (нижней на рисунке) на пылинку, то сила, действующая со стороны всей нити на пылинку, равна .

Подставив в это уравнение , найдём

.

Интегрирование проводится по длине нити, но так как она бесконечна, то

.

Здесь было введено обозначение .

(Для нахождения интеграла воспользуемся следующей заменой: . Тогда , . Значит, .

Так как , то , откуда .

. Значит, 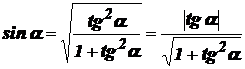. А так как l > 0 и r₀ > 0, то . (Или так как , то tg a > 0.) Следовательно, .

Переходя (возвращаясь опять) от a к y, получаем: .)

Из формулы 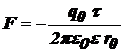следует, что

.

Учитывая, что e = 1, получаем

.

.

Ответ: .

12. С какой силой на единицу длины взаимодействуют две заряженные бесконечно длинные параллельные нити, заряженные с одинаковой линейной плотностью заряда t = 20 мкКл/м, находящиеся на расстоянии R = 10 см друг от друга?

Дано: t₁ = t₂ = t = 20 мкКл/м = 2×10^-5 Кл/м R = 10 см = 0,1 м Решение. Заряды могут быть распространены в пространстве либо дискретно, либо непрерывно. Для характеристики

F_l ‑?

непрерывного распределения электрических зарядов вдоль некоторой линии, по некоторой поверхности или по некоторому объёму вводится понятие о плотности зарядов. Если электрические заряды непрерывно распределены вдоль линии, то вводится линейная плотность зарядов t:

,

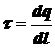где dq – заряд малого участка линии длиной dl.

По условию данной задачи бесконечно длинные нити заряжены с одинаковой линейной плотностью заряда t, значит, электрические заряды непрерывно распределены вдоль этих нитей.

, .

Следовательно, заряд малого участка dl первой нити равен

,

а заряд малого участка dl второй нити равен

.

Рассмотрим первую нить.

Согласно принципу суперпозиции напряжённость электростатического поля, создаваемого непрерывно распределёнными вдоль первой нити зарядами, равна

,

где 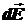‑ напряжённость электростатического поля, создаваемого малым зарядом dq₁, а интегрирование проводится по всем непрерывно распределённым вдоль первой нити зарядам. Малый заряд dq₁ можно считать точечным электрическим зарядом. Следовательно,

,

где ‑ радиус-вектор, проведённый из места нахождения заряда dq₁ в рассматриваемую точку поля.

Рассмотрим теперь взаимодействие первой и второй нитей.

В электростатическом поле первой нити, т.е. системы точечных зарядов dq₁, на точечный заряд dq₂ второй нити действует сила

.

Сила, действующая на всю вторую нить (т.е. суммарная сила, действующая на все равномерно распределённые точечные заряды dq₂ второй нити) в электростатическом поле первой нити, равна

.

Поскольку , , то

,

где интегрирование теперь уже проводится по длинам первой и второй нитей.

, гд l₂ – длина второй нити. Но так как первая и вторая нити бесконечно длинные, то можно принять l₁ = l₂ = l. Тогда

.

Расстояние между точечным зарядом dq₁ первой нити и рассматриваемой точкой поля, т.е. точечным зарядом dq₂ второй нити, можно найти по теореме Пифагора:

r² = R² + l²,

откуда

.

По правилу параллелограмма суммарный вектор сил, действующих со стороны каждого точечного заряда dq₁ первой нити на каждый точечный заряд dq₂ второй нити, перпендикулярен этим параллельным нитям.

Значит, сила, действующая со стороны первой нити на всю вторую нить (или сила, действующая на всю вторую нить в электростатическом поле первой нити), направлена перпендикулярно данным параллельным нитям. Проецируя на перпендикулярное нитям направление (т.е. на ось x на рисунке), получим

.

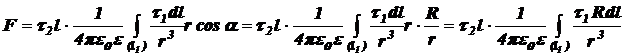Сила на единицу длины, с которой взаимодействуют две заряженные бесконечно длинные нити, равна

.

Подставив в это уравнение , найдём

.

Интегрирование проводится по длине первой нити, но так как она бесконечна, то

.

Здесь было введено обозначение .

Учитывая, что t₁ = t₂ = t, e = 1, получим

.

Ответ: .

13. По тонкому проволочному кольцу равномерно распределён заряд с линейной плотностью t = 100 пКл/м. Определить потенциал j электрического поля в центре кольца.

Дано: t = 100 пКл/м = 10^-10 Кл/м Решение. Разобьём кольцо на N точечных элементов. Потенциал поля i-го точечного заряда:

j ‑?

,

где r_i – расстояние от i-го заряда до той точки поля, в которой необходимо определить потенциал. Так как по условию задачи потенциал электрического поля требуется определить в центре кольца, то для любого i:

r_i = R,

где R ‑ радиус кольца.

Так как поле образовано N точечными зарядами, то потенциал поля (в данном случае в центре кольца) равен алгебраической сумме потенциалов полей, образованных в этой точке (в центре кольца) каждым зарядом отдельно:

,

где q – заряд всего кольца.

Линейная плотность заряда для равномерно заряженной нити (или, в данном случае, равномерно заряженного тонкого проволочного кольца):

,

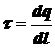откуда

,

где ‑ длина проволоки кольца.

Значит,

.

.

Ответ: .

14. Какой минимальной скоростью 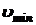должен обладать протон, чтобы он смог достигнуть поверхности положительно заряженного металлического шара, имеющего потенциал j = 400 В. Начальное расстояние протона от поверхности шара r = 3R. R – радиус шара.

Дано: j = 400 В r = 3R Решение. Пусть протон перемещается из точки B в точку C в электрическом поле, созданном заряженным шаром. Работа по перемещению заряда в электрическом поле

‑?

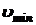A_эл_. = q (j_B - j_C).

Учитывая, что потенциалы поля, образованного заряженным шаром, в точках B и C равны соответственно

и ,

получаем .

По условию задачи потенциал положительно заряженного металлического шара равен j, значит, 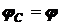, или . Откуда следует, что .

Следовательно, .

Так как работа, совершённая полем, при перемещении заряда из точки B в точку C пошла на изменение кинетической энергии заряженной частицы:

A_эл. = DE_к,

причём , , так как протон и шар одинаково заряжены, и, следовательно, они отталкиваются, что приводит к замедлению протона и, в конце концов, к его остановке, то

,

откуда .

По условию задачи r = 3R. Значит,

.

.

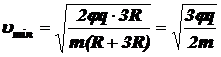Ответ: .

15. Батарея аккумулятора с ЭДСe = 12 В замкнута на два последовательно соединённых реостата, каждый сопротивлением R_р = 5 кОм. Что покажет вольтметр, присоединённый к клеммам одного реостата, если сопротивление вольтметра: 1) R_в = 100 кОм, 2) R_в = 10 кОм? Внутренним сопротивлением аккумулятора пренебречь.

Дано: e = 12 В R_р = 5 кОм = 5×10³ Ом 1) R_в = 100 кОм = 10⁵ Ом 2) R_в = 10 кОм = 10⁴ Ом r = 0 Решение. При последовательном соединении проводников общее сопротивление равно сумме сопротивлений отдельных проводников: .

U ‑?

Так как по условию задачи два реостата соединены последовательно, то

R = R_р + R_р = 2R_р.

По закону Ома для замкнутой цепи ток, протекающий через реостаты до присоединения вольтметра, равен

.

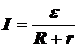Учитывая, что R = 2R_р, r = 0, получаем

.

При параллельном присоединении вольтметра к одному из реостатов вольтметр покажет напряжение

,

где I_в – ток, который потечёт через вольтметр, I_р – ток, который потечёт через реостат.

По первому правилу Кирхгофа алгебраическая сумма токов, сходящихся в узле, равна нулю:

,

где n – число токов. Направления токов выбираются произвольно с учётом того, чтобы в алгебраическую сумму входили как положительные, так и отрицательные токи. Токи, подходящие к узлу, считаются положительными, токи, отходящие от узла, -‑ отрицательными. Значит,

I – I_в – I_р = 0,

где I – ток, подходящий к узлу, I_в, I_р – токи, отходящие от узла.

Выражая из вышенаписанного уравнения I_р и подставляя его в равенство , получим

,

откуда

.

Таким образом, вольтметр, присоединённый к клеммам одного реостата, покажет напряжение

.

1) ;

2) .

Ответ: 1) ; 2) .

16. Сила тока в проводнике изменяется по закону I = I₀ sin wt. Определить количество теплоты Q, которое выделится в проводнике за время, равное половине периода T, если I₀ = 10 А, w = 100 p с^-1.

Дано: I = I₀ sin wt I₀ = 10 А w = 100 p с^-1 Решение. При прохождении электрического тока по проводникам они нагреваются. Согласно закону Джоуля-Ленца количество теплоты dQ, выделяющейся в проводнике за малое время dt, пропорционально квадрату силы тока I, электрическому сопротивлению R проводника и промежутку времени dt: dQ = I²Rdt.

Q ‑?

Интегрируя левую и правую части уравнения, получим

,

где учтено, что период колебаний .

или , где R – численное значение выраженного в единицах СИ – в Ом ‑ сопротивления проводника.

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: