Примеры решения задач 6 страница

Следовательно, магнитная индукция в центре витка

.

.

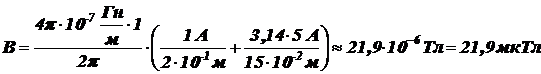Ответ: .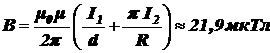

27. Электрон, обладая скоростью 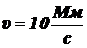, влетел в однородное магнитное поле перпендикулярно линиям магнитной индукции. Индукция магнитного поля B = 0,1 мТл. Определить нормальное и тангенциальное ускорения электрона.

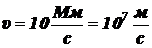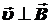
Дано: B = 0,1 мТл = 10-4 Тл	Решение. Для графического изображения стационарного, т.е. не изменяющегося со временем, магнитного поля пользуются методом линий магнитной индукции. Линиями магнитной индукции (силовыми линиями магнитного поля) называются линии, проведённые в магнитном поле так, что в каждой точке поля касательная
an ‑? at ‑?

к линии магнитной индукции совпадает с направлением вектора магнитной индукции в этой точке поля. Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не возвращаясь вторично в любую точку поверхности. Последний случай осуществляется, например, в магнитном поле, создаваемом системой из кругового тока и бесконечного прямолинейного проводника с током, проходящего через центр кругового витка с током, перпендикулярно к его плоскости.

Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение.

На заряженную частицу (частицу с электрическим зарядом q), движущуюся в магнитном поле со скоростью , действует 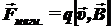– сила Лоренца.

По второму закону Ньютона

,

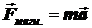где m – масса заряженной частицы,

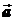‑ ускорение заряженной частицы.

Влетев в однородное магнитное поле, заряженная частица начинает двигаться по окружности, поскольку её скорость перпендикулярна силе Лоренца. Движение частицы по окружности можно представить как движение со скоростью 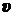под действием силы Лоренца в плоскости, перпендикулярной индукции поля .

В однородном магнитном поле, направленном перпендикулярно к скорости частицы (а в данной задаче как раз 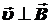), частица равномерно движется по окружности, плоскость которой перпендикулярна вектору . Следовательно,

a_t = 0.

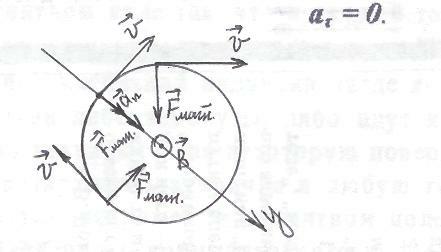
Запишем для заряженной частицы второй закон Ньютона в проекции на ось y:

F_{магн. y} = ma_y,

где

.

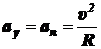Здесь R – радиус окружности.

Так как 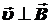, то

F_магн. = quB 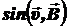= quB sin 90⁰ = quB.

F_{магн y.} = quB.

Значит,

,

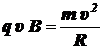откуда

.

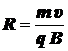Следовательно,

.

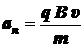По условию данной задачи заряженной частицей является электрон.

Значит,

q = e.

Таким образом, нормальное ускорение электрона

.

.

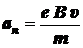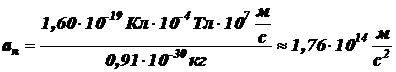Ответ: ; a_t = 0.

28. В однородном магнитном поле перпендикулярно линиям магнитной индукции движется прямой проводник длиной 40 см. Определить силу Лоренца, действующую на свободный электрон проводника, если возникающая на его концах разность потенциалов составляет 10 мкВ.

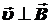
Дано: l = 40 см = 4×10-1м Dj = 10 мкВ = 10-5В	Решение. Для графического изображения стационарного, т.е. не изменяющегося со временем, магнитного поля пользуются методом линий магнитной индукции. Линиями магнитной индукции (силовыми линиями магнитного
FЛ ‑?

поля) называются линии, проведённые в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора магнитной индукции в этой точке поля. Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не возвращаясь вторично в любую точку поверхности. Последний случай осуществляется, например, в магнитном поле, создаваемом системой из кругового тока и бесконечного прямолинейного проводника с током, проходящего через центр кругового витка с током, перпендикулярно к его плоскости.

Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение. В противном случае магнитное поле называется неоднородным.

Потоком вектора магнитной индукции (магнитным потоком) сквозь малую поверхность площадью dS называется физическая величина

,

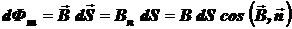где ‑ вектор площадки,

‑ единичный вектор нормали к площадке dS,

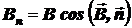‑ проекция вектора на направление нормали (вектор ).

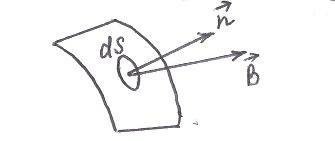
Малая площадка dS выбирается так, чтобы её можно было считать плоской, а значения вектора всюду в её пределах – одинаковыми.

Магнитный поток сквозь произвольную поверхность S:

.

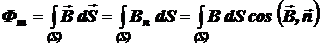При вычислении этого интеграла векторы нормалей к площадкам dS нужно направлять в одну и ту же сторону по отношению к поверхности S. Например, если поверхность S замкнутая, то векторы должны быть либо все внешними нормалями, либо все внутренними нормалями. Если магнитное поле однородно, а поверхность S плоская, то

.

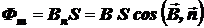Электромагнитной индукцией называется возникновение электродвижущей силы в проводнике при его перемещении в магнитном поле либо в замкнутом проводящем контуре вследствие его движения в магнитном поле или изменения самого поля. Эта электродвижущая сила e_инд. называется электродвижущей силой электромагнитной индукции. Под её влиянием в замкнутом проводнике возникает электрический ток, называемый индукционным током.

Опытами Фарадея было установлено, что электродвижущая сила (ЭДС) индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур проводника.

Закон электромагнитной индукции (закон Фарадея ‑ Максвелла): ЭДС e_инд. электромагнитной индукции в контуре пропорциональна и противоположна по знаку скорости изменения магнитного потока Ф_m сквозь поверхность, натянутую на этот контур, т.е.

.

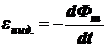При этом несущественно, чем именно вызвано изменение магнитного потока – деформацией контура, его перемещением в магнитном поле или изменением самого поля с течением времени. Направление обхода контура при вычислении e_инд. и направление нормали при вычислении Ф_m должны быть согласованы по правилу правого винта: из конца вектора обход контура должен быть виден происходящим против часовой стрелки.

Знак «‑» в правой части закона электромагнитной индукции соответствует правилу Ленца: при всяком изменении магнитного потока сквозь поверхность, натянутую на замкнутый проводящий контур, в контуре возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению магнитного потока, вызвавшему индукционный ток.

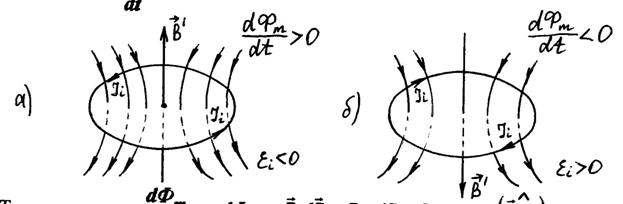
На нижеприведённом рисунке показаны направления индукционного тока I_i в замкнутом контуре и вектора магнитной индукции 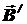магнитного поля индукционного тока для двух случаев: усиления внешнего магнитного поля (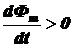, рис. а) и его ослабления (, рис. б).

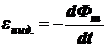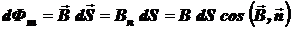Так как , а , то

.

.

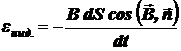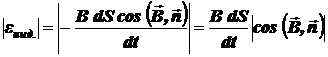Так как 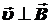, то вектор магнитной индукции перпендикулярен к плоскости рамки; вектор тоже перпендикулярен к плоскости рамки ( ‑ вектор нормали к площадке dS). Следовательно,

.

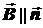Векторы и либо сонаправлены, либо противоположно направлены. Если и сонаправлены (), то 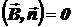и, следовательно, 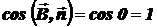, 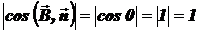. Если и противоположно направлены (), то 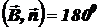и, следовательно, , .

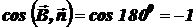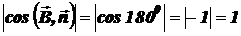Видно, что, если 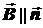, то неважно, сонаправлены ли векторы и или противоположно направлены. В любом случае

.

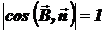Значит,

.

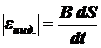Найдём, по какому закону изменяется площадь поверхности S контура, пронизываемой потоком вектора магнитной индукции (магнитным потоком), при движении прямого проводника.

При движении прямого проводника площадь поверхности контура, пронизываемой потоком вектора магнитной индукции (магнитным потоком) изменяется по закону:

dS = l dx,

где l – длина проводника,

dx – перемещение проводника.

Следовательно,

,

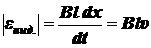где u ‑ скорость движения проводника.

Таким образом, ЭДС индукции, возникающая в прямом проводнике длины l, движущемся с постоянной скоростью u, перпендикулярной к этому проводнику, в однородном магнитном поле с индукцией , равна

.

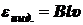Обобщённый закон Ома для произвольного участка цепи AC имеет вид:

IR_AC = U_AC = (j_A ‑ j_C) + e_AC,

где R_AC – сопротивление между точками A и C;

U_AC ‑ напряжение между точками A и C;

(j_A ‑ j_C) – разность потенциалов на концах участка AC;

e_AC – ЭДС всех источников электрической энергии, включенных на участке цепи AC.

В такой форме закон Ома применим как для пассивных участков цепи, не содержащих источников электрической энергии, так и для активных участков, содержащих такие источники.

В неразветвлённой замкнутой электрической цепи сила тока во всех сечениях одинакова, а сама цепь является участком с совпадающими концами 1 и 2 (см. рис. ниже). В такой цепи j₁ = j₂ и R₁₂ = R – общее сопротивление всей цепи.

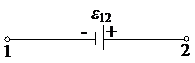
Закон Ома для замкнутой электрической цепи:

IR = e,

где e ‑ алгебраическая сумма всех ЭДС, приложенных в цепи.

Если замкнутая цепь состоит из источника электрической энергии с ЭДС e, и внутренним сопротивлением r, а сопротивление внешней части цепи равно R, то закон Ома имеет вид

.

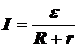Разность потенциалов на клеммах источника равна напряжению на внешней части цепи:

j₁ ‑ j₂ = RI = e ‑ Ir.

Если цепь разомкнута (а в данной задаче цепь разомкнута; в данной задаче рассматривается движение прямого проводника), то тока в ней нет (I = 0), а разность потенциалов на клеммах источника равна его ЭДС:

j₁ ‑ j₂ = e.

Таким образом, разность потенциалов равна ЭДС индукции:

Dj = e_инд..

Значит,

,

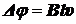откуда

.

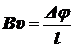На заряженную частицу q, движущуюся в магнитном поле со скоростью 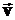, действует 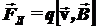– сила Лоренца.

По условию задачи заряженной частицей является свободный электрон. Значит,

q = e.

Так как прямой проводник движется со скоростью 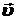, то со скоростью 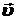движется и свободный электрон проводника:

.

Следовательно,

.

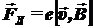Так как 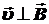, то

F_Л = euB 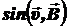= euB sin 90⁰ = euB.

Подставляя 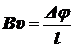в F_Л = euB, получаем силу Лоренца, действующую на свободный электрон проводника:

.

.

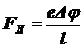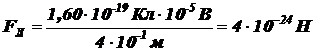Ответ: .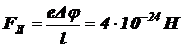

29. Электрон, влетев в однородное магнитное поле с магнитной индукцией B = 2 мТл, движется по круговой орбите радиусом R = 15 см. Определить магнитный момент p_m эквивалентного кругового тока.

ниями магнитной индукции (силовыми линиями магнитного поля) называются линии, проведённые в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора магнитной индукции в этой точке поля. Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не возвращаясь вторично в любую точку поверхности. Последний случай осуществляется, например, в магнитном поле, создаваемом системой из кругового тока и бесконечного прямолинейного проводника с током, проходящего через центр кругового витка с током, перпендикулярно к его плоскости.

Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение.

Движение заряженной частицы по окружности эквивалентно круговому току, а магнитный момент контура с током

p_m = IS,

где S – площадь, охватываемая контуром,

I – ток, текущий по контуру.

Значит, подставляя в это уравнение выражение для тока

,

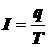где q – заряд частицы,

T – период обращения частицы по орбите,

получим

.

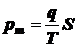Так как заряженная частица движется по круговой орбите радиусом R, то S – площадь, ограниченная окружностью, описываемой заряженной частицей, ‑ равна

S = pR².

Длина окружности

l = 2pR,

а

uT = l,

где u ‑ скорость заряженной частицы, движущейся в магнитном поле.

Следовательно,

2pR = uT,

откуда

.

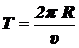Значит,

.

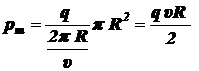На заряженную частицу в магнитном поле действует – сила Лоренца.

По второму закону Ньютона

,

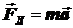где m – масса заряженной частицы,

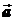‑ ускорение заряженной частицы.

Влетев в однородное магнитное поле, заряженная частица начинает двигаться по круговой орбите, поскольку её скорость перпендикулярна силе Лоренца. Движение частицы по круговой орбите можно представить как движение по окружности со скоростью 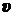под действием силы Лоренца в плоскости, перпендикулярной индукции поля .

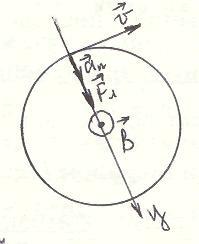
Запишем для заряженной частицы второй закон Ньютона в проекции на ось y:

F_{Л y} = ma_y,

где

.

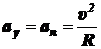Здесь R – радиус окружности.

Так как 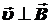, то

F_Л = quB 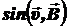= quB sin 90⁰ = quB.

F_{Л y} = quB.

Значит,

,

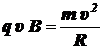откуда

.

Следовательно, магнитный момент p_m эквивалентного кругового тока

.

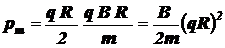По условию данной задачи заряженной частицей является электрон.

Значит,

q = e.

Таким образом,

.

.

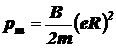Ответ: .

30. Электрон, обладая скоростью 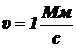, влетает в однородное магнитное поле под углом a = 60⁰ к направлению поля и начинает двигаться по спирали. Напряжённость магнитного поля 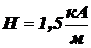. Определить: 1) шаг спирали; 2) радиус витка спирали.

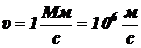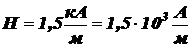
Дано: a = 600	Решение. Для графического изображения стационарного, т.е. не изменяющегося со временем, магнитного поля пользуются методом линий магнитной индукции. Линиями магнитной индукции (силовыми линиями магнитного поля) называются линии, проведённые в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с
1) h ‑? 2) R ‑?

направлением вектора магнитной индукции в этой точке поля. Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не возвращаясь вторично в любую точку поверхности. Последний случай осуществляется, например, в магнитном поле, создаваемом системой из кругового тока и бесконечного прямолинейного проводника с током, проходящего через центр кругового витка с током, перпендикулярно к его плоскости.

Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение.

Движение заряженной частицы (в данном случае электрона) по спирали можно представить как движение по окружности со скоростью 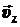под действием силы Лоренца в плоскости, перпендикулярной индукции поля , и равномерное движение вдоль поля со скоростью 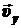(см. рис.). Другими словами, разложим скорость заряженной частицы, влетающей в магнитное поле, по двум направлениям: вдоль линий поля (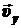) и нормально к ним (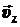). Тогда полная скорость заряженной частицы

.

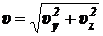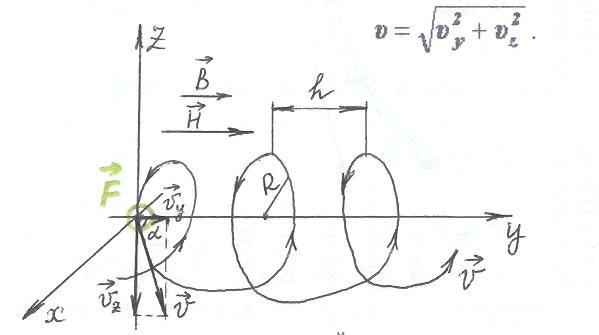
По закону независимости действия сил проекция траектории на плоскость, перпендикулярную к магнитным линиям (к линиям индукции магнитного поля, или к линиям магнитной индукции), будет такая же, как траектория заряженной частицы, влетающей перпендикулярно к полю (к вектору индукции магнитного поля , или к вектору магнитной индукции ) со скоростью 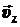, а вдоль поля (вдоль линий индукции магнитного поля, или вдоль линий магнитной индукции) заряженная частица будет перемещаться со скоростью .

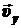Не нашли, что искали? Воспользуйтесь поиском: